Учитывая линейную функцию f (x), как получить квадратичную контрольную точку Безье

Я провел много исследований по этой теме и нашел пару сообщений, которые были полезны, но я просто не могу получить это правильно.

Я разрабатываю очень простое приложение для структурного анализа. В этом приложении мне нужно отобразить график, показывающий внутреннее напряжение луча. График получается по формуле: 

y = (100 * X / 2) * (L - X)

Где L - известная длина луча (для простоты назовем ее 1). И X - это значение между 0 и длиной луча be. Таким образом, окончательная формула будет быть: 

y = (100 * X / 2) * (1 - x) where  0 < X < 1.

Предполагая, что мои начальная и конечная точки являются P0 = (0,0) и P2 = (1,0). Как я могу получить P2 (контрольную точку)?? Я искал на странице Википедии, но я не уверен, как получить контрольную точку из квадратичной формулы кривой Безье: 

B(t) = (1 - t)^2 * P0 + 2*(1 - t)*t * P1 + t^2 * P2

Я уверен, что это должно быть такая легкая проблема, чтобы исправить... может кто-нибудь помочь мне?

P.S.: Я также нашел это, Как найти математическую функцию, определяющую кривую Безье , которая, кажется, объясняет, как сделать обратное о том, чего я пытаюсь достичь. Я просто не могу понять, как это изменить.
2 4
language-agnostic bezier

2 ответа:

Мы хотим, чтобы квадратичная кривая, определенная y, соответствовала квадратичной кривой Безье определяется B(t).

Среди множества точек, которые должны совпадать, есть пик, который происходит в x = 0.5. Когда x = 0.5, 

y = (100 * x / 2) * (1 - x)

    100     1      25
y = ---- * ---  = ---- = 12.5
     4      2       2
Поэтому давайте договоримся для B(0.5) = (0.5, 12.5): 
B(t) = (1-t)^2*(0,0) + 2*(1-t)*t*(Px, Py) + t^2*(1,0)
(0.5, 12.5) = B(0.5) = (0,0) + 2*(0.5)*(0.5)*(Px, Py) + (0.25)*(1,0)

0.5 = 0.5 * Px + 0.25
12.5 = 0.5 * Py

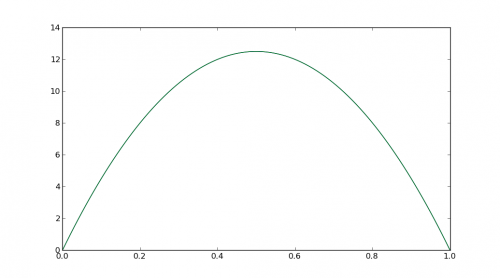
Решая для Px и Py, получим 

(Px, Py) = (0.5, 25)

И вот визуальное подтверждение (в Python), что мы нашли правильную точку: 

# test.py
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 1, 100)
y = (100*x/2)*(1-x)
t = np.linspace(0, 1, 100)
P0 = np.array([0,0])
P1 = np.array([0.5,25])
P2 = np.array([1,0])
B = ((1-t)**2)[:,np.newaxis]*P0 + 2*((1-t)*t)[:,np.newaxis]*P1 + (t**2)[:,np.newaxis]*P2
plt.plot(x, y)
plt.plot(B[:,0], B[:,1])
plt.show()

Запустив python test.py, мы видим, что две кривые перекрываются:

Введите описание изображения здесь

Как я узнал, что нужно выбрать t = 0.5 в качестве значения параметра, когда B(t) достигает своей максимальной высоты?

Ну, в основном это было основано на интуиции, но вот более формальный способ доказать это:

Y-компонент B'(t) равен 0, Когда B(t) достигает своей максимальной высоты. Итак, взяв производную от B(t), мы видим 

0 = 2*(1-2t)*Py
t = 0.5 or Py = 0

Если Py = 0, то B (t) - горизонтальная линия от (0,0) до (1,0). Отвергая этот вырожденный случай, мы видим, что B(t) достигает своей максимальной высоты, когда t = 0.5.

4

Ваша квадратичная формула кривой Безье имеет опечатку в среднем члене. Так и должно быть:
B(t) = (1 - t)^2 * P0 + 2 * (1 - t) * t * P1 + t^2 * P2
Это означает, что вы должны взять P1=(1,50), который нашел @unutbu, и разделить координаты пополам, чтобы получить P1=(.5,25). (Это не будет иметь значения, если вы строите параметрическое уравнение самостоятельно, но если вы хотите что-то вроде LaTeX \qbezier(0,0)(.5,25)(1,0), то вам понадобится скорректированная точка.)

Управляющая точка P1 определяется так, что касательные линии в P0 и P2 пересекаются в P1. Какие средства что если (P1)x=(P2)x, то график должен быть вертикальным с правой стороны (чего вы не хотите).

В ответ на ваш комментарий, если у вас есть квадратичная y=f(x), то она симметрична относительно своей оси (почти тавтологически). Таким образом, максимум/минимум будет происходить в среднем по корням (а также в контрольной точке).
2