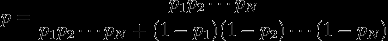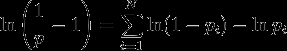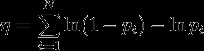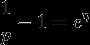Проблема с точностью работы с плавающей запятой в C

Question

Проблема с точностью работы с плавающей запятой в C

Для одного из моих курсовых проектов я начал реализовывать "наивный байесовский классификатор" в C. мой проект заключается в реализации приложения классификатора документов (особенно спама) с использованием огромных обучающих данных.

Теперь у меня есть проблема с реализацией алгоритма из-за ограничений в типе данных C.

(алгоритм, который я использую, приведен здесь, http://en.wikipedia.org/wiki/Bayesian_spam_filtering )

ПОСТАНОВКА ЗАДАЧИ: Алгоритм включает в себя взятие каждого слова в документ и вычисление вероятности того, что он является спам-словом. Если Р1, Р2, Р3 .... pn-вероятности слов-1, 2, 3 ... n. вероятность того, что doc является спамом или нет, вычисляется с помощью

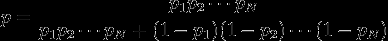
текст Alt

Здесь значение вероятности может быть очень легко около 0,01. Так что даже если я использую тип данных "double", мой расчет пойдет на бросок. Чтобы подтвердить это, я написал пример кода, приведенный ниже.

#define PROBABILITY_OF_UNLIKELY_SPAM_WORD     (0.01)
#define PROBABILITY_OF_MOSTLY_SPAM_WORD     (0.99)

int main()
{
    int index;
    long double numerator = 1.0;
    long double denom1 = 1.0, denom2 = 1.0;
    long double doc_spam_prob;

    /* Simulating FEW unlikely spam words  */
    for(index = 0; index < 162; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_UNLIKELY_SPAM_WORD;
        denom1    = denom1*(long double)(1 - PROBABILITY_OF_UNLIKELY_SPAM_WORD);
    }
    /* Simulating lot of mostly definite spam words  */
    for (index = 0; index < 1000; index++)
    {
        numerator = numerator*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom2    = denom2*(long double)PROBABILITY_OF_MOSTLY_SPAM_WORD;
        denom1    = denom1*(long double)(1- PROBABILITY_OF_MOSTLY_SPAM_WORD);
    }
    doc_spam_prob= (numerator/(denom1+denom2));
    return 0;
}

Я пробовал Float, double и даже long double типы данных, но все та же проблема.

Следовательно, скажем, в документе 100K words, который я анализирую, если только 162 слова имеют вероятность спама 1%, а оставшиеся 99838 явно являются спам-словами, то все равно мое приложение будет говорить это как не спам doc из-за ошибки точности (поскольку числитель легко идет к нулю)!!!.

Это первый раз, когда я сталкиваюсь с такой проблемой. Так как же именно следует решать эту проблему?

6 15

floating-point machine-learning spam-prevention

6 ответов:

Это часто происходит в машинном обучении. АФАИК, ты ничего не можешь поделать с потерей точности. Поэтому, чтобы обойти это, мы используем функцию log и преобразуем деления и умножения в вычитания и сложения, соотв.

Поэтому я решил сделать математику,
Исходное уравнение таково:

Я немного изменяю его:

Ведение журналов на обоих стороны:

Пусть,

Подстановка,

Отсюда альтернативная формула для вычисления комбинированной вероятности:

Если вам нужно, чтобы я расширил это, пожалуйста, оставьте комментарий.

19

Вот хитрость:
for the sake of readability, let S := p_1 * ... * p_n and H := (1-p_1) * ... * (1-p_n), 
then we have:

  p = S / (S + H)
  p = 1 / ((S + H) / S)
  p = 1 / (1 + H / S)

let`s expand again:

  p = 1 / (1 +  ((1-p_1) * ... * (1-p_n)) / (p_1 * ... * p_n))
  p = 1 / (1 + (1-p_1)/p_1 * ... * (1-p_n)/p_n)
Таким образом, в основном, вы получите произведение довольно больших чисел (между 0 и, для p_i = 0.01, 99). Идея состоит в том, чтобы не перемножать тонны малых чисел друг с другом, чтобы получить, ну, 0, а сделать частное из двух малых чисел. Например, если n = 1000000 and p_i = 0.5 for all i, то приведенный выше метод даст вам 0/(0+0), который является NaN, тогда как предлагаемый метод даст вам 1/(1+1*...1), который является 0.5.

Вы можете получить еще лучшие результаты, когда все p_i отсортируйте и соедините их в противоположном порядке (предположим p_1 < ... < p_n), тогда следующая формула получит еще большую точность:
  p = 1 / (1 + (1-p_1)/p_n * ... * (1-p_n)/p_1)
Таким образом, Вы разделяете большие числители (малые p_i) с большими знаменателями (большие p_(n+1-i)) и малые числители с малыми знаменателями.
Редактировать: MSalter предлагаемой полезной дальнейшая оптимизация его ответа. Используя его, формула выглядит следующим образом:
  p = 1 / (1 + (1-p_1)/p_n * (1-p_2)/p_(n-1) * ... * (1-p_(n-1))/p_2 * (1-p_n)/p_1)

4

Попробуйте вычислить обратную величину 1 / p, которая даст вам уравнение вида 1 + 1/(1-p1)*(1-p2)...

Если вы затем подсчитаете возникновение каждой вероятности-похоже, что у вас есть небольшое число значений, которые повторяются-вы можете использовать функцию pow ()-pow(1-p, occurences_of_p)*pow(1-q, occurences_of_q) - и избегать индивидуального округления с каждым умножением.

2

Вы можете использовать вероятность в процентах или промилах:
doc_spam_prob= (numerator*100/(denom1+denom2));
Или
doc_spam_prob= (numerator*1000/(denom1+denom2));
Или использовать какой-то другой коэффициент

1

Я не силен в математике, поэтому не могу комментировать возможные упрощения формулы, которые могли бы устранить или уменьшить вашу проблему. Однако я знаком с ограничениями точности длинных двойных типов и знаю о нескольких произвольных и расширенных математических библиотеках точности для C. Проверьте:

Http://www.nongnu.org/hpalib/ и http://www.tc.umn.edu/~ringx004/mapm-main.html

0

MSalters · Accepted Answer · 2010-04-23 11:43:52

Ваша проблема вызвана тем, что вы собираете слишком много терминов без учета их размера. Одно из решений-взять логарифмы. Другой - сортировать ваши индивидуальные термины. Для начала перепишем уравнение в виде 1/p = 1 + ∏((1-p_i)/p_i). Теперь ваша проблема заключается в том, что некоторые термины маленькие, а другие большие. Если у вас слишком много маленьких терминов подряд, вы будете недополучать, а с слишком большим количеством больших терминов вы будете переполнять промежуточный результат.
Итак, не ставьте слишком много одинаковых элементов в ряд. Сортировать термины (1-p_i)/p_i. В результате первый член будет самым маленьким, а последний-самым большим. Теперь, если бы вы умножили их сразу, у вас все равно был бы недостаточный поток. Но порядок расчета не имеет значения. Используйте два итератора во временной коллекции. Один начинается в начале (т. е. (1-p_0)/p_0), другой-в конце (т. е. (1-p_n)/p_n), а ваш промежуточный результат начинается с 1.0. Теперь, когда ваш промежуточный результат > = 1.0, вы берете термин спереди, а когда ваш промежуточный результат
В результате, когда вы берете термины, промежуточный результат будет колебаться вокруг 1.0. Он будет только подниматься или опускаться, когда у вас закончатся маленькие или большие термины. Но это нормально. В этот момент вы потребили крайности на обоих концах, поэтому промежуточный результат будет медленно приближаться к конечному результату.
Конечно, существует реальная возможность переполнения. Если входная информация полностью не является спамом (p=1E-1000), то 1/p переполнится, потому что ∏((1-p_i)/p_i) переполняет. Но поскольку термины отсортированы, мы знаем, что промежуточный результат переполнит только, Если ∏((1-p_i)/p_i) переполнится. Таким образом, если промежуточный результат переполняется, то нет никакой последующей потери точности.