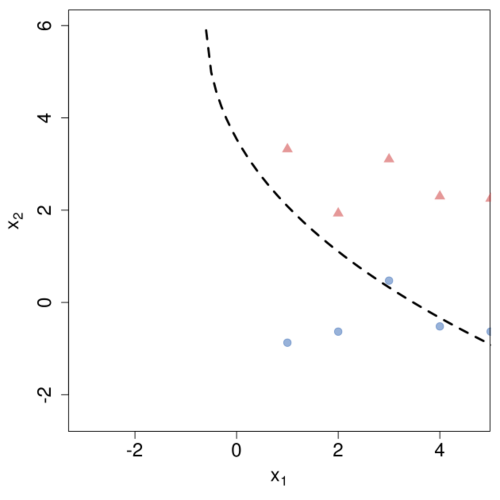
Построение границы решения двух многомерных гауссовских уравнений
Я пытаюсь построить что-то похожее на ниже:
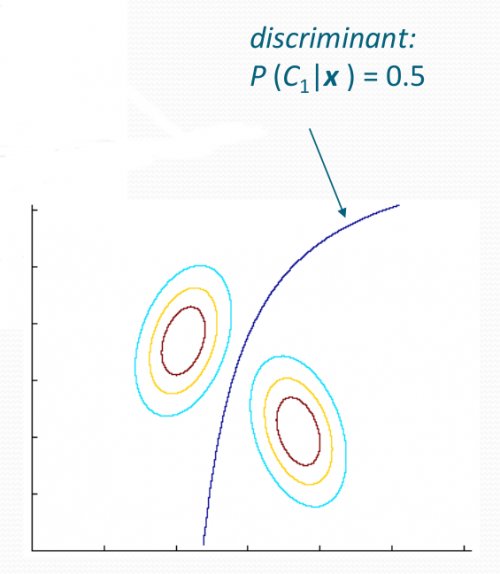
Я использую Matlab. Я добился рисования контурных участков. Однако я не мог нарисовать дискриминанта. Может ли кто-нибудь показать пример кода Matlab или дать какую-то идею, чтобы нарисовать дискриминант?
2 ответа:
Если вы знаете функцию плотности вероятности каждого Гаусса для данной точки
(x,y), скажем ееpdf1(x,y)иpdf2(x,y), то вы можете просто построить контурную линиюf(x,y) := pdf1(x,y) > pdf2(x,y). Таким образом, вы определяете функциюfкак1iffpdf1(x,y)>pdf2(x,y). Таким образом, единственный контур будет помещен вдоль кривой, гдеpdf1(x,y)==pdf2(x,y), которая является границей решения (дискриминантом). Если вы хотите определить" красивую " функцию, вы можете сделать это просто установивf(x,y) = sgn( pdf1(x,y) - pdf2(x,y) ), и построение ее контурного графика приведет к тому же самому дискриминантный.
Вот как я решил бы эту задачу аналитически: вы приравниваете эти две дискриминантные функции
g1(x)=x' W1 x + w1' x + w10 g2(x)=x' W2 x + w2' x + w20 g1(x) = g2(x) ==> x' (W2 - W1) x + (w2-w1)'x + w20 - w10Тогда я считаю, что W2-W1 - это матрица
W2-W1 = [a b; c d]Который затем, расширяя вектор x=[x1 x2]', получим:
a x1^2 + (b+c) x1 x2 + d x2^2 + (w21-w11) x1 + (w22-w12) x2 + w20-w10 = 0Это уравнение эллипса, поэтому вы можете упростить его в следующем виде:
(x1 - a0)^2/h + (x2-b0)^2/g = r^2Или, можно предположить, что вы знаете диапазон x1, например x1=[-2: 0.1:2], а затем решить параболу