Построение графиков с использованием кривых Безье
У меня есть массив точек (x0,y0)... (xn,yn) монотонных в x и я хочу нарисовать "лучшую" кривую через них, используя кривые Безье. Эта кривая не должна быть слишком " зубчатой "(например, похожей на соединение точек) и не слишком извилистой (и определенно не"идти назад"). Я создал прототип, но задаюсь вопросом, существует ли объективно "лучшее решение".
xi,y1 x(i+1)y(i+1). Мой текущий подход (за исключением конечных точек) для сегмента x(i), x(i+1) это:
- найти вектор
x(i-1)...x(i+1), нормализовать и масштабировать его наfactor * len(i,i+1), чтобы получить вектор для ведущей контрольной точки - найти вектор
x(i+2)...x(i), нормализовать и масштабировать его наfactor * len(i,i+1), чтобы получить вектор для конечной контрольной точки.
Я попробовал коэффициент=0.1 (слишком неровный), 0.33 (слишком пышный) и 0.20 - примерно правильно. Но есть ли лучший подход, который (скажем) делает 2-ю и 3-ю производные как можно более гладкими. (Я предполагаю, что такой алгоритм реализован в графике пакеты)?
Я могу опубликовать псевдо / код, если потребуется. Вот эти три изображения (0.1/0.2/0.33). Контрольные точки показаны прямыми линиями: черной (замыкающей) и красной (ведущей)
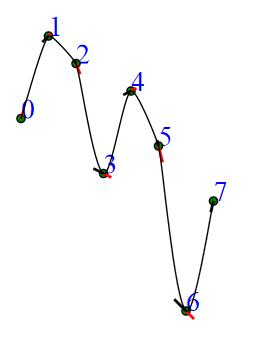


Вот текущий код. Он направлен на построение Y против X (монотонный X) без close-ing. Я построил свою собственную библиотеку для создания SVG (preferred output); этот код создает тройки x,y в coordArray для каждой кривой сегмент (control1, xcontrol2, end). Начало предполагается последней операцией (перемещение или кривая). Это Java, но должно быть легко интерпретируемо (CurvePrimitive отображает кубический, "d" - строковое представление полного пути в SVG).
List<SVGPathPrimitive> primitiveList = new ArrayList<SVGPathPrimitive>();
primitiveList.add(new MovePrimitive(real2Array.get(0)));
for(int i = 0; i < real2Array.size()-1; i++) {
// create path 12
Real2 p0 = (i == 0) ? null : real2Array.get(i-1);
Real2 p1 = real2Array.get(i);
Real2 p2 = real2Array.get(i+1);
Real2 p3 = (i == real2Array.size()-2) ? null : real2Array.get(i+2);
Real2Array coordArray = plotSegment(factor, p0, p1, p2, p3);
SVGPathPrimitive primitive = new CurvePrimitive(coordArray);
primitiveList.add(primitive);
}
String d = SVGPath.constructDString(primitiveList);
SVGPath path1 = new SVGPath(d);
svg.appendChild(path1);
/**
*
* @param factor to scale control points by
* @param p0 previous point (null at start)
* @param p1 start of segment
* @param p2 end of segment
* @param p3 following point (null at end)
* @return
*/
private Real2Array plotSegment(double factor, Real2 p0, Real2 p1, Real2 p2, Real2 p3) {
// create p1-p2 curve
double len12 = p1.getDistance(p2) * factor;
Vector2 vStart = (p0 == null) ? new Vector2(p2.subtract(p1)) : new Vector2(p2.subtract(p0));
vStart = new Vector2(vStart.getUnitVector().multiplyBy(len12));
Vector2 vEnd = (p3 == null) ? new Vector2(p2.subtract(p1)) : new Vector2(p3.subtract(p1));
vEnd = new Vector2(vEnd.getUnitVector().multiplyBy(len12));
Real2Array coordArray = new Real2Array();
Real2 controlStart = p1.plus(vStart);
coordArray.add(controlStart);
Real2 controlEnd = p2.subtract(vEnd);
coordArray.add(controlEnd);
coordArray.add(p2);
// plot controls
SVGLine line12 = new SVGLine(p1, controlStart);
line12.setStroke("red");
svg.appendChild(line12);
SVGLine line21 = new SVGLine(p2, controlEnd);
svg.appendChild(line21);
return coordArray;
}
2 ответа:
Кривая Безье требует наличия точек данных, а также наклона и кривизны в каждой точке. В графической программе наклон задается наклоном управляющей линии, а кривизна визуализируется длиной.
Когда у вас нет таких управляющих линий, вводимых пользователем, вам нужно оценить градиент и кривизну в каждой точке. Страница Википедии http://en.wikipedia.org/wiki/Cubic_Hermite_spline , и в частности раздел "интерполяция набора данных" имеет формула, которая принимает эти значения непосредственно.
Как правило, оценка этих значений из точек выполняется с использованием конечной разности - поэтому вы используете значения точек с обеих сторон, чтобы помочь оценить. Единственный выбор здесь-как обращаться с конечными точками, где есть только одна смежная точка: вы можете установить кривизну на ноль, или если кривая периодическая, вы можете "обернуть" и использовать значение последней точки.
Страница Википедии, на которую я ссылался, также имеет другие схемы, но большинство других вводят какой-то другой "свободный параметр", который вам нужно будет найти способ настройки, поэтому в отсутствие дополнительной информации, которая поможет вам решить, как установить другие параметры, я бы пошел на простую схему и посмотрел, нравятся ли вам результаты.
Дайте мне знать, если статья в Википедии недостаточно ясна, и я придумаю какой-нибудь код.Еще один момент, который нужно знать: какого рода интерполяцию Безье вы ищете? Большинство графических программ делают кубический Безье в 2-х измерениях (т. е. можно нарисовать кругообразную кривую), но ваши образцы изображений выглядят так, как будто это может быть аппроксимация 1D функций (например, для каждого x существует только одно значение y). Графическая кривая типа программы На самом деле не упоминается на странице, на которую я ссылался. Математика, используемая для преобразования оценки наклона и кривизны в управляющий вектор вида, иллюстрированного на http://en.wikipedia.org/wiki/B%C3%A9zier_curve (кубический Безье) потребует некоторой проработки, но идея аналогична.
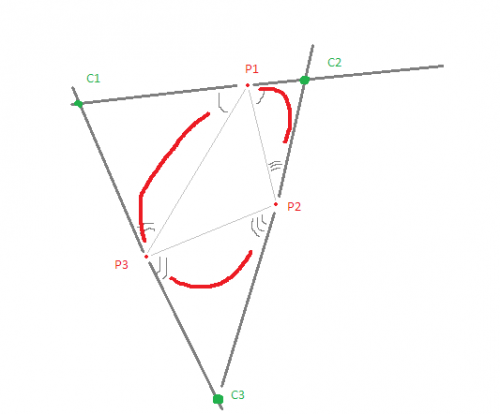
Ниже находится рисунок и алгоритм для возможной схемы, предполагая, что ваш единственный вход - это три точки P1, P2, P3
Постройте линию (C1,P1,C2) так,чтобы углы (P3,P1,C1) и (P2, P1, C2) были равны. Подобным же образом строятся и другие темно-серые линии. Пересечения этих темно-серых линий (обозначенных C1, C2 и C3) становятся контрольными точками как в том же смысле, что и изображения на кривой Безье сайта Википедии. Таким образом, каждая красная кривая, такая как (P3, P1), является квадратичная кривая Безье, определяемая точками (P3, C1, P1). Построение Красной кривой аналогично приведенному на сайте Википедии.
Однако я замечаю, что вектор управления на странице Википедии кривая Безье, похоже, не соответствует тому типу вектора управления, который вы используете, поэтому вам, возможно, придется выяснить, как уравнять два подхода.
Я попытался сделать это с помощью квадратичных сплайнов вместо кубических, что упрощает выбор контрольных точек (вы просто выбираете градиент в каждой точке, чтобы он был взвешенным средним средних градиентов соседних интервалов, а затем рисуете касательные к кривой в точках данных и вставляете контрольные точки, где эти касательные пересекаются), но я не смог найти разумную политику для установки градиентов конечных точек. Поэтому я выбрал установку Лагранжа вместо этого:
function lagrange(points) { //points is [ [x1,y1], [x2,y2], ... ] // See: http://www.codecogs.com/library/maths/approximation/interpolation/lagrange.php var j,n = points.length; var p = []; for (j=0;j<n;j++) { p[j] = function (x,j) { //have to pass j cos JS is lame at currying var k, res = 1; for (k=0;k<n;k++) res*=( k==j ? points[j][1] : ((x-points[k][0])/(points[j][0]-points[k][0])) ); return res; } } return function(x) { var i, res = 0; for (i=0;i<n;i++) res += p[i](x,i); return res; } }С этим я просто делаю много образцов и соединяю их прямыми линиями.
Это все еще неверно, если ваши данные (как и мои) состоят из измерений реального мира. Они подвержены случайным ошибкам, и если вы используете технику, которая заставляет кривую попадать в них точно, то вы можете получить глупые долины и холмы между точками. В таких случаях вы должны спросить себя, какой порядок полинома данные должны соответствовать и ... хорошо... именно это я и собираюсь сделать. иди разберись.