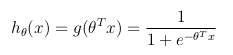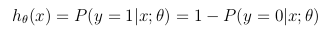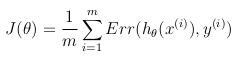Почему функция затрат логистической регрессии имеет логарифмическое выражение?

Функция затрат для логистической регрессии равна 

cost(h(theta)X,Y) = -log(h(theta)X) or -log(1-h(theta)X)
Мой вопрос заключается в том, на чем основано логарифмическое выражение для функции стоимости .Откуда она берется? я верю, что вы не можете просто взять и поставить "бревно" из ниоткуда. Если бы кто-нибудь мог объяснить вывод функции стоимости, я был бы благодарен. спасибо.
3 22
machine-learning logarithm logistic-regression

3 ответа:

Источник : мои собственные заметки, сделанные во время курса машинного обучения Стэндфорда в Coursera , Эндрю Нг. Все заслуги перед ним и этой организацией. Курс свободно доступен для любого, кто может пройти его в своем собственном темпе. Изображения сделаны мной с помощью LaTeX (формулы) и R (графика).

Функция гипотезы

Логистическая регрессия используется, когда переменная y , которую требуется предсказать, может принимать только дискретные значения (т. е.: классификация).

Рассматривая двоичную классификационную задачу (y может принимать только два значения), то имея набор параметров θ и набор входных признаков x , функция гипотезы может быть определена так, что ограничена между [0, 1], в которой g () представляет сигмоидную функцию:

Введите описание изображения здесь

Эта гипотетическая функция одновременно представляет собой оценочную вероятность того, что y = 1 на входе x параметризовано θ :

Введите описание изображения здесь

Функция затрат

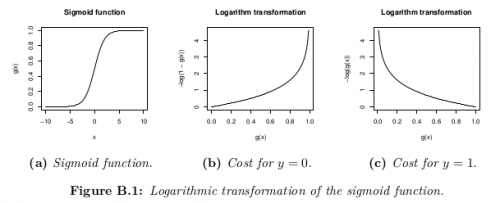
Функция затрат представляет собой цель оптимизации.

Введите описание изображения здесь

Хотя возможным определением функции стоимости может быть среднее Евклидово расстояние между гипотезой h_θ(x) и фактическим значением y среди всехM выборок в обучающем множестве, пока функция гипотезы формируется с помощью сигмоидная функция, это определение приведет к невыпуклой функции затрат, Что означает, что локальный минимум может быть легко найден до достижения глобального минимума. Для того чтобы функция затрат была выпуклой (и, следовательно, обеспечивала сходимость к глобальному минимуму), Функция затрат преобразуется с помощью логарифма сигмоидной функции.

Введите описание изображения здесь

Таким образом, целевая функция оптимизации может быть определена как среднее затраты/ошибки в обучающем наборе:

Введите описание изображения здесь

42

Эта функция затрат является просто переформулировкой критерия максимального(логарифмического)правдоподобия.

Модель логистической регрессии выглядит следующим образом: 

P(y=1 | x) = logistic(θ x)
P(y=0 | x) = 1 - P(y=1 | x) = 1 - logistic(θ x)

Вероятность записывается как: 

L = P(y_0, ..., y_n | x_0, ..., x_n) = \prod_i P(y_i | x_i)

Логарифмическая вероятность равна: 

l = log L = \sum_i log P(y_i | x_i)

Мы хотим найти θ, которое максимизирует вероятность: 

max_θ \prod_i P(y_i | x_i)

Это то же самое, что максимизировать логарифмическую вероятность: 

max_θ \sum_i log P(y_i | x_i)

Мы можем переписать это как минимизацию стоимости C= - l: 

min_θ \sum_i - log P(y_i | x_i)
  P(y_i | x_i) = logistic(θ x_i)      when y_i = 1
  P(y_i | x_i) = 1 - logistic(θ x_i)  when y_i = 0
12

Мое понимание (не 100% эксперт здесь, я могу ошибаться) состоит в том, что log может быть грубо объяснено как невыполнение exp, которое появляется в Формуле для гауссовой плотности вероятности. (Вспомните -log(x) = log(1/x).)

Если я правильно понимаю Бишопа [1]: Когда мы предполагаем, что наши положительные и отрицательные обучающие выборки происходят из двух разных гауссовых кластеров (разное расположение, но одинаковая ковариация), то мы можем разработать идеальный классификатор. И этот классификатор выглядит так же, как логистическая регрессия (например, граница линейного решения). Конечно, следующий вопрос заключается в том, почему мы должны использовать классификатор, который является оптимальным для разделения гауссовых кластеров, когда наши обучающие данные часто выглядят по-разному? Распознавание образов и машинное обучение, Кристофер М. Бишоп, глава 4.2 (вероятностные генеративные модели)
7