Реализация Арксинус CORDIC не
Недавно я внедрил библиотеку CORDIC-функций для уменьшения требуемой вычислительной мощности (мой проект основан на PowerPC и чрезвычайно строг в своих спецификациях времени выполнения). Язык - ANSI-C.
Другие функции (sin / cos / atan) работают в пределах точности как в 32, так и в 64-битных реализациях.К сожалению, функция asin () систематически терпит неудачу для некоторых входных данных.
Для целей тестирования я реализовал .h файл, используемый в S-функции simulink. (Это только для моего удобства, вы можете скомпилировать следующее как автономное .exe с минимальными изменениями)
Кордик.h:
#include <stdio.h>
#include <stdlib.h>
#define FLOAT32 float
#define INT32 signed long int
#define BIT_XOR ^
#define CORDIC_1K_32 0x26DD3B6A
#define MUL_32 1073741824.0F /*needed to scale float -> int*/
#define INV_MUL_32 9.313225746E-10F /*needed to scale int -> float*/
INT32 CORDIC_CTAB_32 [] = {0x3243f6a8, 0x1dac6705, 0x0fadbafc, 0x07f56ea6, 0x03feab76, 0x01ffd55b, 0x00fffaaa, 0x007fff55,
0x003fffea, 0x001ffffd, 0x000fffff, 0x0007ffff, 0x0003ffff, 0x0001ffff, 0x0000ffff, 0x00007fff,
0x00003fff, 0x00001fff, 0x00000fff, 0x000007ff, 0x000003ff, 0x000001ff, 0x000000ff, 0x0000007f,
0x0000003f, 0x0000001f, 0x0000000f, 0x00000008, 0x00000004, 0x00000002, 0x00000001, 0x00000000};
/* CORDIC Arcsine Core: vectoring mode */
INT32 CORDIC_asin(INT32 arc_in)
{
INT32 k;
INT32 d;
INT32 tx;
INT32 ty;
INT32 x;
INT32 y;
INT32 z;
x=CORDIC_1K_32;
y=0;
z=0;
for (k=0; k<32; ++k)
{
d = (arc_in - y)>>(31);
tx = x - (((y>>k) BIT_XOR d) - d);
ty = y + (((x>>k) BIT_XOR d) - d);
z += ((CORDIC_CTAB_32[k] BIT_XOR d) - d);
x = tx;
y = ty;
}
return z;
}
/* Wrapper function for scaling in-out of cordic core*/
FLOAT32 asin_wrap(FLOAT32 arc)
{
return ((FLOAT32)(CORDIC_asin((INT32)(arc*MUL_32))*INV_MUL_32));
}
Это можно назвать примерно так:
#include "Cordic.h"
#include "math.h"
void main()
{
y1 = asin_wrap(value_32); /*my implementation*/
y2 = asinf(value_32); /*standard math.h for comparison*/
}
Результаты таковы, как показано:
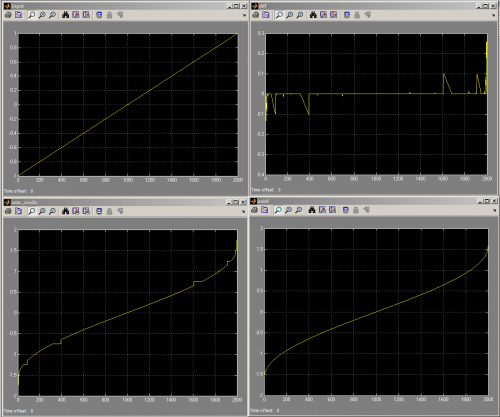
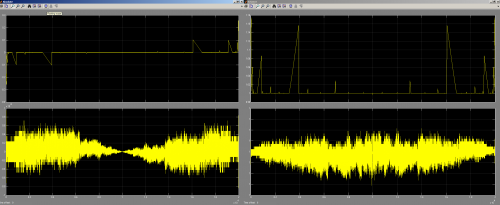
Вверху слева показан вход [-1;1] с 2000 шагов (0.001 инкременты), нижний левый выход моей функции, нижний правый стандартный выход и верхний правый разность двух выходов.
Сразу видно, что ошибка не укладывается в 32-битную точность.
Я проанализировал шаги, выполняемые (и промежуточные результаты) моим кодом, и мне кажется, что в определенный момент значение y "достаточно близко" к исходному значению arc_in , и то, что может быть связано с битовым сдвигом, приводит к решению проблемы. расходиться.
Мои вопросы:
- Я в недоумении, является ли эта ошибка неотъемлемой частью реализации CORDIC или я сделал ошибку в реализации? Я ожидал снижения точности вблизи экстремумов, но эти всплески в середине довольно неожиданны. (наиболее заметные из них находятся сразу за
- Если это что-то из сердечной реализации, существуют ли известные обходные пути?
+/- 0.6, но даже после них есть больше при меньших значениях, хотя и не столь выраженных)
Редактировать:
-
Поскольку некоторые комментарии упоминают об этом, да, я проверил определение
INT32, даже написав#define INT32 int32_Tне изменяет результаты ни на малейшую величину. -
Время вычисления на целевом оборудовании измерялось сотнями повторений блока из 10.000 итераций функции со случайным вводом в диапазоне допустимости. Наблюдаемые средние результаты (для одного вызова функции) таковы: следует:
math.h asinf() 100.00 microseconds CORDIC asin() 5.15 microseconds
(по-видимому, предыдущий тест был ошибочным, новый перекрестный тест получил не лучше, чем в среднем 100 микросекунд по всему диапазону достоверности) -
Я, видимо, нашел лучшую реализацию. Его можно скачать в версии matlab здесь и в C здесь. Я более подробно проанализирую его внутреннюю работу и сообщу об этом позже.
3 ответа:
Чтобы рассмотреть несколько вещей, упомянутых в комментариях:
- данный код выводит значения, идентичные другойКОРДИЧЕСКОЙ реализации . Сюда же относятся и заявленные неточности.
Самая большая ошибка - это когда вы приближаетесь кarcsin(1). Вторая по величине ошибка состоит в том, что значения отarcsin(0.60726)доarcsin(0.68514)все возвращают0.754805.- есть некоторые неясные ссылки на неточности в методе Кордика для некоторых функций, включая arcsin. Данное решение состоит в том, чтобы выполнить "двойные итерации", хотя я не смог заставить это работать (все значения дают большое количество ошибок).
- альтернативная сердечная имплементацияимеет комментарий
/* |a| < 0.98 */в реализации arcsin (), который, по-видимому, подтверждает, что есть известные неточности, близкие к 1.В качестве грубого сравнения нескольких различных методов рассмотрим следующие результаты (все тесты выполнены на настольном компьютере, компьютере Windows7 с использованием MSVC++ 2010, бенчмарки синхронизировано с использованием 10м итераций в диапазоне arcsin () 0-1):
- вопрос КОРДИЧЕСКИЙ код: 1050 МС, ошибка 0.008 авг, максимальная ошибка 0.173
- альтернативный код CORDIC (Реф): 2600 МС, ошибка 0.008 компания AVG, 0.173 максимальная ошибка
- код ATAN() CORDIC: 2900 МС, 0.21 средняя ошибка, 0.28 максимальная ошибка
- CORDIC с использованием двойных итераций: 4700 МС, 0.26 средняя ошибка, 0.917 максимальная ошибка (???)
- математический встроенный asin (): 200 мс, 0 средняя ошибка, 0 максимальная ошибка
- рациональное приближение (ref): 250 ms, 0.21 средняя ошибка, 0.26 максимальная ошибка
- линейный поиск таблицы (см. ниже) 100 мс, 0.000001 средняя ошибка, 0.00003 максимальная ошибка
- серия Тейлора (7-я степень, ref): 300 мс, 0,01 средняя ошибка, 0,16 максимальная ошибка
Эти результаты находятся на рабочем столе, поэтому насколько они релевантны для встроенной системы-хороший вопрос. Если сомневаетесь, будет рекомендовано провести профилирование/сравнительный анализ по соответствующей системе. Большинство проверенных решений не имеют очень хорошей точности в диапазоне (0-1), и все, кроме одного, на самом деле медленнее, чем встроенная функция
asin().Линейный код поиска таблицы размещен ниже и является моим обычным методом для любой дорогостоящей математической функции, когда скорость желательна по сравнению с точностью. Он просто использует таблицу элементов 1024 с линейной интерполяцией. По-видимому, это самый быстрый и самый точный из всех испытанных методов., хотя встроенный
asin()на самом деле не намного медленнее (протестируйте его!). Его можно легко отрегулировать для большей или меньшей точности путем изменения размера таблицы.// Please test this code before using in anything important! const size_t ASIN_TABLE_SIZE = 1024; double asin_table[ASIN_TABLE_SIZE]; int init_asin_table (void) { for (size_t i = 0; i < ASIN_TABLE_SIZE; ++i) { float f = (float) i / ASIN_TABLE_SIZE; asin_table[i] = asin(f); } return 0; } double asin_table (double a) { static int s_Init = init_asin_table(); // Call automatically the first time or call it manually double sign = 1.0; if (a < 0) { a = -a; sign = -1.0; } if (a > 1) return 0; double fi = a * ASIN_TABLE_SIZE; double decimal = fi - (int)fi; size_t i = fi; if (i >= ASIN_TABLE_SIZE-1) return Sign * 3.14159265359/2; return Sign * ((1.0 - decimal)*asin_table[i] + decimal*asin_table[i+1]); }
Арксин "одиночного поворота" сильно ошибается, когда аргумент просто больше начального значения 'x', где это магический масштабирующий коэффициент - 1/An ~= 0.607252935 ~= 0x26DD3B6A.
Это происходит потому, что для всех аргументов > 0 Первый Шаг Всегда имеет y = 0
Если arg
Если arg > 1 / An, то d = +1, и этот шаг отодвигается все дальше от правильного ответа, а для диапазона значений чуть больше 1 / An все последующие шаги имеют d = -1, но не могут исправить результат :-(
Я нашел:
arg = 0.607 (ie 0x26D91687), relative error 7.139E-09 -- OK arg = 0.608 (ie 0x26E978D5), relative error 1.550E-01 -- APALLING !! arg = 0.685 (ie 0x2BD70A3D), relative error 2.667E-04 -- BAD !! arg = 0.686 (ie 0x2BE76C8B), relative error 1.232E-09 -- OK, againОписания метода предупреждают об abs (arg) >= 0.98 (или около того), и я обнаружил, что где-то после 0.986 процесс не сходится и относительная ошибка скачет до ~5E-02 и достигает 1E-01 (!!) при arg=1 :- (
Как и вы, я также обнаружил, что для 0,303Итак... единственный поворот CORDIC для arcsine выглядит для меня ерундой :- (
Добавлено позже... когда я еще внимательнее присмотрелся к единичному вращающемуся КОРДИКУ, то обнаружил еще много небольших областей, где относительная погрешность велика...
... поэтому я бы не касайтесь этого как метода вообще... это не просто мусор, этобесполезно .
Кстати: я очень рекомендую "руководство по программному обеспечению для элементарных функций", William Cody and William Waite, Prentice-Hall, 1980. Методы вычисления функций уже не так интересны (но требуется тщательное практическое обсуждение соответствующих сокращений диапазона). Однако для каждой функции они дают хорошую процедуру проверки.
Дополнительный источник, который я связал в конце вопроса, по-видимому, содержит решение.
Предлагаемый код можно свести к следующему:#define M_PI_2_32 1.57079632F #define SQRT2_2 7.071067811865476e-001F /* sin(45°) = cos(45°) = sqrt(2)/2 */ FLOAT32 angles[] = { 7.8539816339744830962E-01F, 4.6364760900080611621E-01F, 2.4497866312686415417E-01F, 1.2435499454676143503E-01F, 6.2418809995957348474E-02F, 3.1239833430268276254E-02F, 1.5623728620476830803E-02F, 7.8123410601011112965E-03F, 3.9062301319669718276E-03F, 1.9531225164788186851E-03F, 9.7656218955931943040E-04F, 4.8828121119489827547E-04F, 2.4414062014936176402E-04F, 1.2207031189367020424E-04F, 6.1035156174208775022E-05F, 3.0517578115526096862E-05F, 1.5258789061315762107E-05F, 7.6293945311019702634E-06F, 3.8146972656064962829E-06F, 1.9073486328101870354E-06F, 9.5367431640596087942E-07F, 4.7683715820308885993E-07F, 2.3841857910155798249E-07F, 1.1920928955078068531E-07F, 5.9604644775390554414E-08F, 2.9802322387695303677E-08F, 1.4901161193847655147E-08F, 7.4505805969238279871E-09F, 3.7252902984619140453E-09F, 1.8626451492309570291E-09F, 9.3132257461547851536E-10F, 4.6566128730773925778E-10F}; FLOAT32 arcsin_cordic(FLOAT32 t) { INT32 i; INT32 j; INT32 flip; FLOAT32 poweroftwo; FLOAT32 sigma; FLOAT32 sign_or; FLOAT32 theta; FLOAT32 x1; FLOAT32 x2; FLOAT32 y1; FLOAT32 y2; flip = 0; theta = 0.0F; x1 = 1.0F; y1 = 0.0F; poweroftwo = 1.0F; /* If the angle is small, use the small angle approximation */ if ((t >= -0.002F) && (t <= 0.002F)) { return t; } if (t >= 0.0F) { sign_or = 1.0F; } else { sign_or = -1.0F; } /* The inv_sqrt() is the famous Fast Inverse Square Root from the Quake 3 engine here used with 3 (!!) Newton iterations */ if ((t >= SQRT2_2) || (t <= -SQRT2_2)) { t = 1.0F/inv_sqrt(1-t*t); flip = 1; } if (t>=0.0F) { sign_or = 1.0F; } else { sign_or = -1.0F; } for ( j = 0; j < 32; j++ ) { if (y1 > t) { sigma = -1.0F; } else { sigma = 1.0F; } /* Here a double iteration is done */ x2 = x1 - (sigma * poweroftwo * y1); y2 = (sigma * poweroftwo * x1) + y1; x1 = x2 - (sigma * poweroftwo * y2); y1 = (sigma * poweroftwo * x2) + y2; theta += 2.0F * sigma * angles[j]; t *= (1.0F + poweroftwo * poweroftwo); poweroftwo *= 0.5F; } /* Remove bias */ theta -= sign_or*4.85E-8F; if (flip) { theta = sign_or*(M_PI_2_32-theta); } return theta; }Следует отметить следующее:
На следующем рисунке показаны абсолютные (слева) и относительные ошибки (справа) старой реализации (вверху) по сравнению с реализацией, содержащейся в этом ответе (внизу). Относительная погрешность получается только путем деления выхода CORDIC на выход встроенного математического аппарата.реализация сек. Она строится вокруг
- это КОРДИЧЕСКАЯ реализация "двойной итерации".
Таким образом, таблица- отличается по конструкции от старой таблицы.
- и вычисление выполняется в нотации с плавающей запятой, это приведет к значительному увеличению времени вычисления на целевое оборудование.
- на выходе присутствует небольшое смещение, удаляемое через проход
theta -= sign_or*4.85E-8F;.1, а не0по этой причине.Пик относительная погрешность (при не делении на ноль) равна
1.0728836e-006.Средняя относительная погрешность равна
2.0253509e-007(почти в соответствии с 32-битной точностью).