В d3 можно ли динамически изменить место начала пути для твининга?
Чтобы: уточнить. Представьте себе круг. Мы начинаем рисовать круг с определенной координаты. Теперь давайте нарисуем круг, начиная с другой координаты.
Я играю с данными пути, полученными из глифов SVG, а затем использую d3js tween для анимации изменения между путями.
Для этого примера, считая от 1 - > 9,0 и затем повторяя.
Http://jsfiddle.net/chrisloughnane/HL2ET/
Как вы можете видеть, некоторые переходы не так хороши, как другие. Они рисуют линию, которая закрывает путь для следующего пути. (Я предполагаю, что) это происходит, когда начало и конец пути очень далеки друг от друга, когда производится расчет для новой формы. Когда это работает, это очень приятно.
Может ли кто-нибудь предложить возможное решение этих уродливых линий?Код без данных пути
svg.append("path")
.attr("transform", "translate(150,300)scale(.2,-.2)")
.style("stroke", "red")
.style("fill", "gray")
.style("stroke-width", "9")
.attr("d", d0)
.call(transition, digits[0], digits[position]);
function transition(path, d0, d1) {
position++;
if(position==10)
{
position=0;
}
path.transition()
.duration(2000)
.attrTween("d", pathTween(d1, 4))
.each("end", function() { d3.select(this).call(transition, d1, digits[position]); });
}
function pathTween(d1, precision) {
return function() {
var path0 = this,
path1 = path0.cloneNode(),
n0 = path0.getTotalLength(),
n1 = (path1.setAttribute("d", d1), path1).getTotalLength();
// Uniform sampling of distance based on specified precision.
var distances = [0], i = 0, dt = precision / Math.max(n0, n1);
while ((i += dt) < 1) distances.push(i);
distances.push(1);
// Compute point-interpolators at each distance.
var points = distances.map(function(t) {
var p0 = path0.getPointAtLength(t * n0),
p1 = path1.getPointAtLength(t * n1);
return d3.interpolate([p0.x, p0.y], [p1.x, p1.y]);
});
return function(t) {
return t < 1 ? "M" + points.map(function(p) { return p(t); }).join("L") : d1;
};
};
}
К сожалению, он не работает на chrome mobile тоже где как http://bl.ocks.org/mbostock/3081153 работает отлично.
Следующим шагом является: примените этот эффект к предложениям.
1 ответ:
Разница между вашим примером и примером Бостока состоит в том, что в его примере есть один непрерывный путь, который он превращает в другой непрерывный путь.
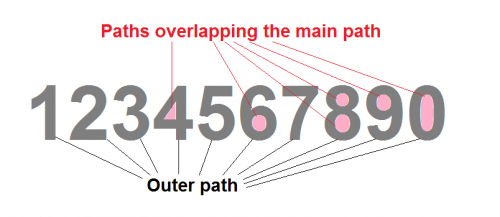
В то время как в вашем примере цифры, такие как 1, 2, 3, 5, 6, 7 может быть нарисован с использованием одного непрерывного пути. Но для того, чтобы нарисовать цифры, такие как 4, 6, 9 и 0, вам нужно 2 пути - один поверх другого. И, для цифры 8, вам нужно иметь 2 пути поверх внешнего пути.
Итак, мое предложение состоит в том, чтобы сохранить 2 пути в любое время поверх внешнего пути, который вы используете в настоящее время, и дайте им соответствующие размеры, когда будет показана какая-либо особая цифра.
См. изображение для получения более подробной информации: