Судоку решатель медленный, нуждается в рассмотрении ограничений ранее
У меня есть NxN Sudoku solver, написанный в прологе. Приведенный ниже код прекрасно работает для решения задачи 4*4. (У меня есть некоторые доменные инфы), но это медленно для 9x9. Я пробовал много способов улучшить функцию create row, то есть уже рассматривал, что каждое значение в строке должно быть уникальным (и должно содержаться в своей области), но они не работали. Как я мог бы улучшить это без библиотекарей?
all_distinct(X) :-
sort(X, Sorted),
length(X, OriginalLength),
length(Sorted, SortedLength),
OriginalLength == SortedLength.
good_by_coulmns(Solution) :- length(Solution, Length),
forall((between(1, Length, X), get_column(Solution, X, Y)),
all_distinct(Y)).
get_area(Solution, X, Y, Z) :- length(Solution, Length),
SQRootF is sqrt(Length),
SQRoot is round(SQRootF),
MinCol is SQRoot * (X-1) + 1,
MinRow is SQRoot * (Y-1) + 1,
matrix_block(MinRow, MinCol, SQRoot, SQRoot, Solution, A), flatten2(A,Z).
good_by_areas(Solution) :- length(Solution, Length),
SQRootF is sqrt(Length), SQRoot is round(SQRootF),
forall((between(1, SQRoot, X), between(1, SQRoot, Y), get_area(Solution, X, Y, Z)),
all_distinct(Z)).
createRow(Solution, Domain, Row) :- maplist(member, Row, Domain),
all_distinct(Row),
good_by_coulmns(Solution).%, write(Solution), nl.
tryToSolve(Domains, Solution) :- length(Solution, L), length(Domains, L), !,
maplist(createRow(Solution), Domains, Solution),
good_by_coulmns(Solution),
good_by_areas(Solution).
Я могу дать недостающие правила, если это необходимо, но это прекрасно работает sofar, поэтому мы можем использовать их как строительные блоки.
1 ответ:
Вопрос скорее об А. И., чем о программировании.
Ну, вам нужны некоторые ограничения для вашего Судоку, чтобы позволить ему работать быстрее. Существует ограничение, однако это большая работа, поэтому я объясню и напишу его в математической форме, и это зависит от того, как вы реализовали свой код, и вы можете легко принять его:
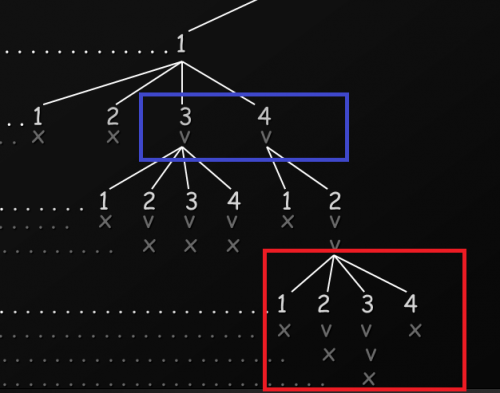
Идея: основная идея заключается в том, что когда вам дают какое-то судоку, то вы можете сразу заполнить несколько мест, так что на многих ветвях программа не будет углубляться а затем потерпеть неудачу, а затем вернуться назад, вместо этого лучше, если он потерпит неудачу на каком-то более высоком узле. Посмотрите на рисунок ниже, Если вы поместите это ограничение, то можно заблокировать путь для Пролога в 6 местах и разрешить его только в 3 местах, потому что каждая строка имеет 9 элементов. Во многих случаях он не будет исследовать узлы, которые я отметил синим цветом.Без ограничений он будет идти вниз до конца, и вы увидите, сколько дополнительных ветвей он исследует.
Но как? мы используйте свойства судоку:
Правила: каждая строка , каждый Колум и каждая сетка имеют уникальные элементы.
Алгоритм: когда вам дают какую-то(судоку-таблицу), то вы должны проверить первые три строки (0,1,2), если в них есть какой-либо элемент, который является одинаковым в любой из двух строк. Например, для каждого элемента из первой строки вы должны проверить, находится ли этот элемент во второй или третьей строке, если нет, то перейдите во вторую строку и попытайтесь найти элемент, который находится во второй и третий ряд. Вот две возможности:
У вас нет совпадения: Если в первых трех строках нет одного и того же элемента, то перейдите к следующим трем строкам (3,4,5) и найдите там, а затем строку (6,7,8).
Примечание: вы должны проверять только те линии, которые образуют сетку(матрицу 3x3) вместе.Например, строки (0,1,2) вместе, затем (3,4,5) вместе, а затем (6,7,8) вместе.
У вас есть совпадение: Предположим, вы нашли совпадение в строках (0,2). Так как каждый строка может иметь уникальный элемент, тогда мы знаем ,что этот элемент должен быть в строке 1 , но как мы узнаем, что результирующая строка равна 1, ну, нам нужна формула. смотрите далее:
Математическая форма: вы всегда можете получить результирующую строку путем вычитания. У нас был матч в строках 0 и 2. Синус эти три строки находятся вместе, поэтому мы берем сумму их номера строки(0 + 1 + 2 = 3). Так как мы работаем с переменными и вы совпадаете в (i = 0 и j = 2) и ваша общая сумма = 3
И
sum- i - j = 1 so the new element should be in row 1. Этот формула всегда верна: думайте, что у вас есть совпадение по номерам строк(i = 4 and j = 5), тогда сумма этих трех номеров строкЯвляется
4 + 5 + 6 = 15и вычитает15 - 4 -5 = 5.однако есть альтернативные способы, но мы работаем с переменной, поэтому нам нужно знать, в какой строке мы должны поместить элемент, из которого у нас есть соответствие в других двух строках.Определение сетки: После того, как вы определили, в какой строке будет лежать ваш новый элемент, следующий шаг-проверить, в какой сетке он будет лежать, потому что каждая строка часть из трех сеток (матриц 3х3). Например, строки 0 содержат элементы (0,1,2) в первой сетке, затем (3,4,5) во второй сетке и затем (6,7,8) в третьей сетке.
Всего у вас есть (9) подсетей и начиная с (0 до 8).
Отношение между подрешетками и строками: у нас есть только информация о строках, поэтому нам нужно найти отношение между строками и номерами сетки. Это матрица NxN, поэтому высота сетки равна ширине сетки (3x3), что означает, что каждые три строки вместе образуют 3 сетки, потому что длина строк равна 9, а длина сетки в 3, поэтому мы получаем 3 сетки высоты 3 и длины 3.Пример: строки (0,1,2) образуют три пояса ,начиная с 0 ,1, 2, а затем строки (4,5,6) из других 3 сеток: gridnumber(4,5,6).
Мы можем получить их номер сетки, сделав это : (предположим, что в строке 0 у нас было совпадение в colum 4 с номером строки 2 и номером colum 2, тогда мы должны получить сетку 0 и сетку 1 (respt), потому что первая сетка-это сетка 0(colum: 0 1 2).
Мы используем эту формулу чтобы получить номер сетки в одномерном списке .
Теперь мы знаем, что сетки 1 и 2 не могут иметь этот элемент, потому что в каждой сетке нам нужен уникальный элемент от 1 до 9. Таким образом, это должна быть сетка 0 , но как получить результирующую сетку, Ну, мы можем получить это снова, взяв сумму трех номеров строк (потому что число строк равно числу сетки), которая равна = 3, и вычесть число сетки других двух сеток, которое было(0+1), тогда мы получим сетку 2.
(mod(x,9)/3) + 3*(x/27)Мы еще не закончили тем не менее, мы должны преобразовать эту вещь в один индекс, потому что мы работаем в основном с одномерным списком. Итак, эта формула дает точное место:
Формула: x = (newRow)*9 + (newGrid)*3 и x - это наше место. Вы можете проверить эту формулу, подключив значения.Теперь мы получаем точные три слота, в которые может быть помещен наш элемент. В этот момент Вы говорите, что либо list[x] = list[i], либо list[x+1] = list[i], либо list[x+2] = list[i].