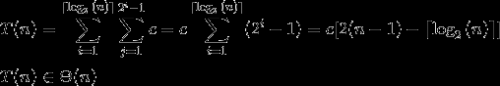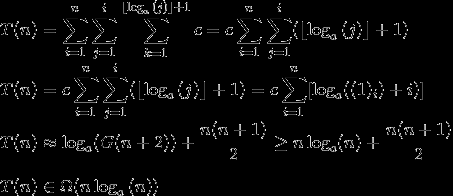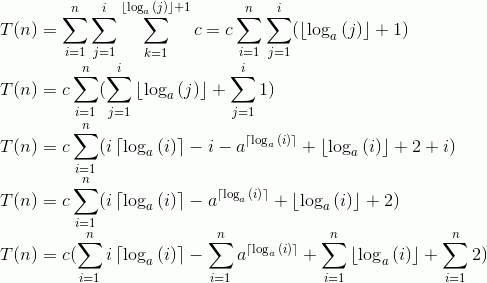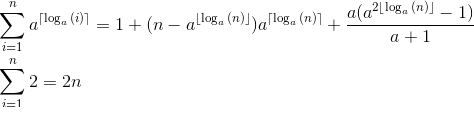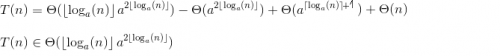сложность для вложенных циклов

Question

сложность для вложенных циклов

Я пытаюсь выяснить сложность цикла for, используя большую нотацию O. Я делал это раньше в других моих классах, но этот более строгий, чем другие, потому что он находится на фактическом алгоритме. Код выглядит следующим образом:

for(i=n ; i>1 ; i/=2) //for any size n
{
    for(j = 1; j < i; j++)
    {
      x+=a
    }
}

И

for(i=1 ; i<=n;i++,x=1) //for any size n
{
    for(j = 1; j <= i; j++)
    {
      for(k = 1; k <= j; x+=a,k*=a)
      {

      }
    }
}

Я пришел к выводу, что первый цикл имеет o(n) сложность, потому что он проходит через список n раз. Что касается второй петли, то я немного заблудился! Спасибо за помощь в анализе. Каждая петля находится в своем собственном пространстве, они не вместе.

3 4

loops big-o complexity-theory asymptotic-complexity nested-loops

3 ответа:

EDIT: я согласен, что первый блок кода - O( n)

Вы уменьшаете внешний цикл i, ныряя на 2, а во внутреннем цикле вы выполняете i раз, так что число итераций будет суммой по всем степеням двух меньше или равно N, но больше 0, то есть n ^{log (n)+1} - 1, Итак, O (n).

Второй блок кода O (log _a(n) n²) предполагая, что a является константой.

Две крайние петли приравниваются к сумме все числа меньше или равны n, то есть n(n-1)/2, поэтому O (n²). Наконец, внутренняя петля-это степени a меньше верхней границы n, которая является O (log_a n).

0

Формально вы можете поступить следующим образом:

Фрагмент 1:

Фрагмент 2 (Почхаммер, G-функция и приближение Стирлинга):

С log (G (n)) .

[Обновление фрагмента 2]:

С некоторыми улучшениями из публикации "дискретные циклы и наихудшая производительность", д-р Johann Blieberger (все случаи проверены для a = 2):

Где:

Следовательно,

0

Deepu · Accepted Answer · 2013-05-25 22:20:41

Рассмотрим первый фрагмент кода,
for(i=n ; i>1 ; i/=2) //for any size n
{
    for(j = 1; j < i; j++)
    {
      x+=a
    }
}
Инструкция x+=a выполняется в общей сложности n + n/2 + n/4 + ... + 1 раз.

Сумма первого журнала₂n членов г. п. с начальным членом n и общим отношением 1/2 является, (n (1-(1/2)^{бревно₂n}))/(1/2). Таким образом, сложность первого фрагмента кода равна O(n).
Теперь рассмотрим второй фрагмент кода,
for(i=1 ; i<=n; i++,x=1)
{
    for(j = 1; j <= i; j++)
    {
      for(k = 1; k <= j; x+=a,k*=a)
      {

      }
    }
}
Две внешние петли вместе называют внутреннюю петлю полной из n(n+1)/2 раз. Самый внутренний цикл выполняется не более log<sub>a</sub>n раз. Таким образом, общая временная сложность второго фрагмента кода равна O(n²log _an) .