Python экспоненциальная / линейная подгонка кривой

Этот вопрос касается не столько программирования, сколько математики, но мне хотелось бы услышать некоторые мнения.

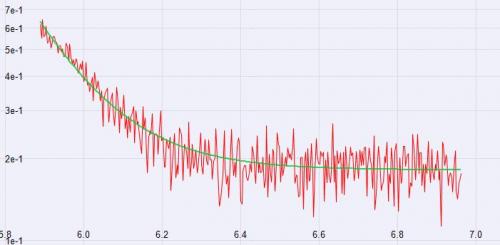
Я пытаюсь смоделировать экспоненциальное поведение спада этой кривой, но, как вы можете видеть, существует определенный уровень флуктуаций/шума при более низких значениях. Как я могу устранить / приглушить этот шум, чтобы моя посадка не зависела от него?

Я работаю с логарифмом этой кривой, поэтому я использую линейные регрессии для подгонки. Я использовал метод наименьших квадратов, но наклон прямой линии существенно изменяется (примерно на 20%) в зависимости от выбранного мной интервала времени.

Я слышал о 2 других методах, которые могли бы помочь:

• взвешенный метод наименьших квадратов, но я не знаю, как я буду взвешивать свои очки.
• наименьшие абсолютные отклонения, очевидно малые значения имеют тенденцию быть менее релевантными при использовании этого метода.

Я хотел бы избежать фазы проб и ошибок. У тебя есть какие-нибудь идеи?

Edit: код является сделано с помощью python