проблемы пространственной точности sql server
У меня возникли проблемы с неточными результатами STIntersects в SQL Server 2008 R2. Возможно, кто - то может пролить свет на то, что я делаю неправильно-я не могу поверить, что это предел точности в пространственных запросах SQL Server?
--example 1
DECLARE @pt1 geography;
DECLARE @pt2 geography;
DECLARE @polygon geography;
SET @polygon = geography::STPolyFromText('POLYGON((-172.0000000000 54.0000000000,-164.0000000000 54.0000000000,-164.0000000000 56.0000000000,-172.0000000000 56.0000000000,-172.0000000000 54.0000000000))',4326);
SET @pt1 = geography::STPointFromText('POINT(-170.0000000000 54.04)',4326);
SET @pt2 = geography::STPointFromText('POINT(-170.0000000000 56.04)',4326);
SELECT @polygon.STIntersects(@pt1); --should be 1, but returns 0 (error is .04 * 60 nautical miles per degree - something like 4.4 km)
SELECT @polygon.STIntersects(@pt2); --should be 0, but returns 1
--example 2
DECLARE @pt1 geography;
DECLARE @pt2 geography;
DECLARE @polygon geography;
SET @polygon = geography::STPolyFromText('POLYGON((-171.0000000000 54.0000000000,-170.0000000000 54.0000000000,-170.0000000000 54.5000000000,-171.0000000000 54.5000000000,-171.0000000000 54.0000000000))',4326);
SET @pt1 = geography::STPointFromText('POINT(-170.5000000000 54.001)',4326);
SET @pt2 = geography::STPointFromText('POINT(-170.5000000000 54.01)',4326);
SELECT @polygon.STIntersects(@pt1); --should be 1, returns 0
SELECT @polygon.STIntersects(@pt2); --should be 1, returns 1 (less error than in example 1, perhaps due to smaller polygon?)
1 ответ:
Нет предела точности как таковой, это чисто до кривой земли, которую использует тип географии. Прямоугольник, который вы нарисовали в Примере 1, на самом деле имеет изогнутые края, а не прямые линии (из-за расстояния по изогнутой поверхности). Горизонтальные края в Северном полушарии естественно изгибаются вверх в середине.
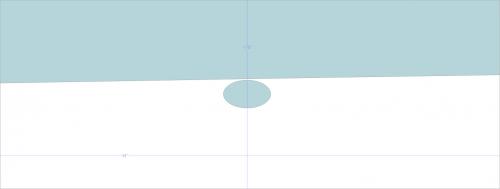
Следовательно, @pt1 всегда будет ложным, потому что он находится вне "изогнутых" ребер многоугольника. Как так (буферизуется, чтобы вы могли видеть точка).
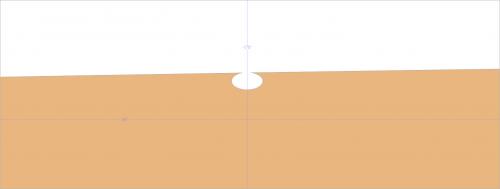
И аналогично, @pt2 фактически находится внутри изогнутого ребра, поэтому всегда будет истинно, как таковое (отображается как буферизованное и как отверстие в многоугольнике).
Если бы вы визуализировали их, используя геометрию (плоскую модель), вы получили бы ответы, которые искали, но не обязательно правильный.