Пример усеченного целочисленного степенного закона в Python?

Какую функцию я могу использовать в Python, если я хочу получить усеченный целочисленный степенной закон?

, то есть, учитывая два параметра a и m, генерируют случайное целое число x в диапазоне [1,m), которое следует распределению, пропорциональному 1/x^a.

Я искал вокруг numpy.random, но я не нашел этого распределения.

2 5
python numpy random distribution

2 ответа:

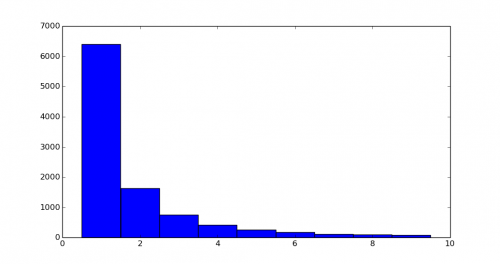
Насколько мне известно, не включает ни составляющей определяет этот дистрибутив для вас. Однако с помощью SciPy легко определить свою собственную дискретную функцию распределения, используя scipy.rv_discrete: 

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

def truncated_power_law(a, m):
    x = np.arange(1, m+1, dtype='float')
    pmf = 1/x**a
    pmf /= pmf.sum()
    return stats.rv_discrete(values=(range(1, m+1), pmf))

a, m = 2, 10
d = truncated_power_law(a=a, m=m)

N = 10**4
sample = d.rvs(size=N)

plt.hist(sample, bins=np.arange(m)+0.5)
plt.show()

Введите описание изображения здесь

3

Я не использую Python, поэтому вместо того, чтобы рисковать синтаксическими ошибками, я попытаюсь описать решение алгоритмически. Это дискретная инверсия грубой силы. Он должен довольно легко переводиться на Python. Я предполагаю, что индексация массива на основе 0.

Настройка:

  1. Создайте массив cdf размера m с cdf[0] = 1 в качестве первой записи, cdf[i] = cdf[i-1] + 1/(i+1)**a для остальных записей.

  2. Масштабируйте все записи, разделив cdf[m-1] на каждую - теперь они действительно CDF ценности.

Использование:

  • генерируйте ваши случайные значения, генерируя равномерное(0,1) и поиск по cdf[], пока вы не найдете запись больше, чем ваш форма. Верните индекс + 1 в качестве вашего x-значения.

Повторите для любого количества x-значений.

Например, с помощью a,m = 2,10 я вычисляю вероятности непосредственно как: 

[0.6452579827864142, 0.16131449569660355, 0.07169533142071269, 0.04032862392415089, 0.02581031931145657, 0.017923832855178172, 0.013168530260947229, 0.010082155981037722, 0.007966147935634743, 0.006452579827864143]

А CDF-это: 

[0.6452579827864142, 0.8065724784830177, 0.8782678099037304, 0.9185964338278814, 0.944406753139338, 0.9623305859945162, 0.9754991162554634, 0.985581272236501, 0.9935474201721358, 1.0]

При генерации, если я получил равномерный результат 0,90 I вернул бы x=4, потому что 0.918... первая запись CDF больше, чем моя форма.

Если вы беспокоитесь о скорости, вы можете построить таблицу псевдонимов, но при геометрическом распаде вероятность досрочного завершения линейного поиска по массиву довольно высока. В приведенном примере, Например, вы закончите на первом взгляде почти 2/3 времени.

3