Я переназначил переходы NFA в вашей диаграмме, поэтому объяснение проще.

Это оставляет вас с регулярным выражением:

 (R1* R2 R3* R4)* R1* R2 R3*

Первый раздел, заключенный в скобки, по существу описывает последовательность шагов, которые приведут вас из q0 обратно в q0. Регулярное выражение говорит: делайте это столько, сколько хотите, и когда вы закончите возиться, вы можете следовать R1 столько раз, сколько хотите, чтобы все еще оставаться в состоянии q0, и когда вы действительно закончите возиться вокруг, следуйте R2, чтобы добраться до конечного состояния, где вы можете петлять на R3 столько, сколько захотите.

Это не самый аккуратный или интуитивно понятный способ, чтобы государство устранило NFA в регулярное выражение, но я думаю, что это правильно. Надеюсь, объяснение имеет смысл. Если нет, спрашивайте в комментариях!

В качестве ссылки я написал регулярное выражение, которое я придумал. Обратите внимание, что я использую | вместо+, как у вас.

(aa|ab(bb)*ba)* (ab(bb)*a|b) ((a(bb)*a)* ((a(bb)*ba|b)(aa|ab(bb)*ba)*(ab(bb)*a|b))*)*

Правка:

Вы хотите, чтобы ваше регулярное выражение захватило все возможные паттерны, которые в конечном итоге приведут вас к конечному состоянию, начиная с состояния q0. Теперь представьте, что вы стоите в состоянии q0. Какие действия вы могли бы предпринять? Вы можете разделить свой набор действий на те, которые удержат вас в состоянии q0, и те, которые приведут вас в состояние q1.

Действия, которые удержат вас в q0:

• Следуйте За R1
• следуйте за R2, делайте все, что вы можете сделать в q1, а затем вернитесь в q0, следуя за R4. Назовем это регулярное выражение R2_R4 где этот пробел должен быть заполнен всеми возможными вещами, которые мы можем сделать в q1, кроме возвращения через R4. Ну, единственное, что мы можем сделать в q1, это следовать R3 кучу раз, поэтому мы заменяем пробел на R2R3*R4.

Перечисляя все способы, которыми вы можете оставаться в q0, вы по существу избавляетесь от перехода от q1 к q0 (R4). Другими словами, вы говорите, что после этой части моего регулярного выражения, если вы перейдете в состояние q1, не должно быть никакого способа вернуться в q0 (если бы это было так захвачен первой частью регулярного выражения). Так что ваш NFA теперь выглядит примерно так:

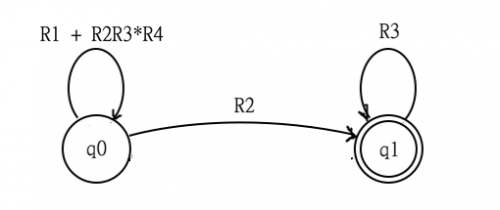
Таким образом, ваше последнее регулярное выражение будет: следуйте переходу, который остается в q0, затем перейдите в q1 через R2 и оставайтесь в q2 столько, сколько вы хотите, следуя R3. Таким образом, ваше регулярное выражение может выглядеть следующим образом:

 (R1 + R2R3*R4)* R1* R2 R3*

Которая на самом деле эквивалентна той, что у вас есть:

 (R1* R2 R3* R4)* R1* R2 R3*

Потому что или природа (R1+R2 R3* R4)* эквивалентна (R1* R2 R3* R4)*. Я на самом деле думаю, что версия с or ( + ) яснее но это не имеет особого значения, пока он работает.