Последовательные и допустимые эвристики
Какой-либо последовательной эвристики является также приемлемым. Но когда эвристика допустима, но не последовательна (монотонна)?
Пожалуйста, приведите пример, в котором это имеет место.
2 ответа:
Как отмечают Рассел и Норвиг в книгеискусственный интеллект: современный подход (наиболее часто используемый учебник ИИ), трудно придумать эвристику, которая допустима, но не последовательна.
Очевидно, вы можете выбрать значения для узлов в графе таким образом, чтобы эвристика, которую они представляют, была допустимой, но не согласованной. В этой статье Felner et al есть хороший пример того, как это возможно, но он немного плотный, поэтому я буду подведем итог:
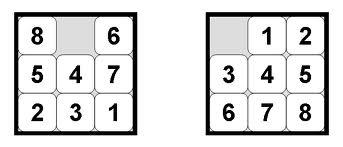
Фельнер и др. также приводят несколько конкретных примеров допустимой, но непоследовательной эвристики. Рассмотрим задачу 8-головоломки:
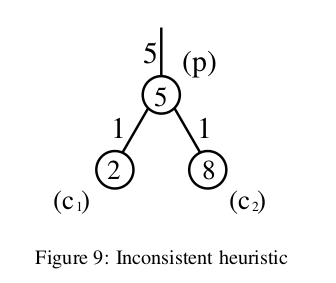
- эта эвристика непоследовательна в
Поскольку этот граф неориентирован, эта эвристика также непоследовательна вc1, потому что она дает более низкую (т. е. менее информативную) нижнюю границу стоимости достижения цели, чем ее родительский узел. Оценка затрат на достижение цели через родительский узел составляет не менее 10 (поскольку стоимость пути кpравна 5, а эвристическая оценка вpтакже равна 5). Оценка затрат на достижение цели черезc1, однако, составляет всего 8 (стоимость родителя (5), плюс стоимость пути от родителя (1), плюс эвристическая оценка приc1(2)).c2, потому что переход отc2кpимеет ту же проблему, что и выше.В этой головоломке есть 8 скользящих плиток, пронумерованных 1-8, и одно пустое место. Плитки начинают выходить из строя (как на изображении слева). Цель состоит в том, чтобы привести головоломку в состояние, показанное выше справа, исключительно путем скольжения плиток в пустое пространство. Классическая эвристика для этой задачи (манхэттенское расстояние каждой плитки до места, где она должна быть) допустима и непротиворечива. Однако вы можете придумать другую эвристику. Может быть, вы просто хотите посмотреть на расстояние Манхэттена (то есть количество квадратов) от 1, 2 и 3 до мест, в которых они находятся. предполагается, что они находятся в состоянии цели. Эвристика, хотя и менее информативна, чем манхэттенское расстояние всех плиток, все же допустима и последовательна. Но предположим, что вы выбрали дополнительную группу квадратов, возможно, 5, 6 и 7. А затем предположим, что способ вычисления эвристики в каждом узле состоит в случайном выборе одного из этих множеств (1,2 и 3) или (5, 6 и 7) и вычислении их Манхэттенского расстояния до места назначения. Эта эвристика все еще допустимый - он может только когда-либо недооценивать или соответствовать количеству ходов, необходимых для достижения состояния цели. Однако это больше не согласуется - нет четкой связи между эвристическими оценками в каждом узле.
Давно умер, но я все равно отдам свои два цента. Я думаю, что намного проще всего думать об этом, что допустимая эвристика говорит, что вы не можете промахнуться, когда добираетесь до определенного узла цели, в то время как последовательная эвристика говорит, что вы не можете промахнуться, когда добираетесь до любого узла. Это делает отношения ясными: поскольку узел цели является некоторым узлом, допустима последовательная эвристика. Но поскольку допустимое гарантирует это свойство только для одного узла, допустимое не подразумевает консистенция.