Поиск нормального вектора для устройства iOS

Я хотел бы использовать CMAttitude, чтобы узнать вектор, нормальный к стеклу экрана iPad / iPhone (относительно Земли). Таким образом, я бы получил векторы, подобные следующим:

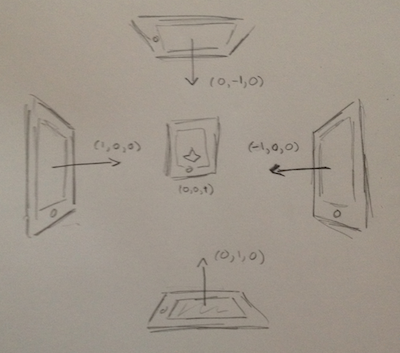
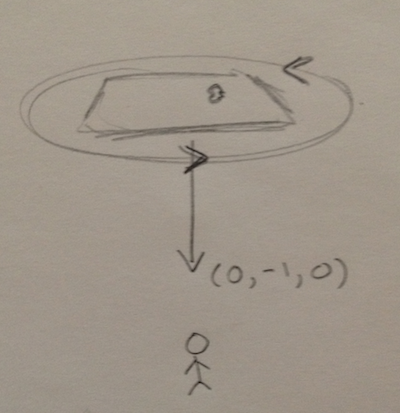
Введите описание изображения здесь

Обратите внимание, что это отличается от ориентации, так как мне все равно, как устройство вращается вокруг оси Z. Поэтому, если бы я держал iPad над головой вниз,он бы читал (0, -1,0), и даже когда я вращал его над головой (как вертолет), он продолжал бы читать (0,-1,0):

Введите описание изображения здесь

Я чувствую, что это может быть довольно легко, но так как я новичок в кватернионах и не до конца понимаю параметры системы отсчета для движения устройства, он избегал меня весь день.

2 25
ios core-motion gyroscope

2 ответа:

  1. в вашем случае мы можем сказать, что вращение устройства равно вращению нормального устройства (вращение вокруг самого нормального просто игнорируется, как вы его указали)
  2. CMAttitude который вы можете получить через CMMotionManager.deviceMotion обеспечивает вращение относительно системы отсчета . Его свойства кватернионов, Ротора матричные и Эйлеровы углы - это просто разные представления.
  3. опорная рамка может быть задана при запуске устройства обновление движения с помощью метода CMMotionManager startDeviceMotionUpdatesUsingReferenceframe. До iOS 4 Вы должны были использовать multiplyByInverseOfAttitude

Собрав все это вместе, вы просто должны умножить кватернион правильным образомс нормальным вектором, когда устройство лежит лицом вверх на столе. Теперь нам нужен этот правильный способ умножения кватернионов, представляющий вращение: согласно вращающимся векторам это делается автор:

N = q * e * q', где q - кватернион, поставляемый CMAttitude [w, (x, y, z)], q' - его сопряженный [w, (- x, - y, - z)] и e - кватернионное представление лицевой нормали [0, (0, 0, 1)]. К сожалению, CMQuaternion от Apple-это struct, и поэтому вам нужен небольшой вспомогательный класс.

Quaternion e = [[Quaternion alloc] initWithValues:0 y:0 z:1 w:0];
CMQuaternion cm = deviceMotion.attitude.quaternion;
Quaternion quat = [[Quaternion alloc] initWithValues:cm.x y:cm.y z:cm.z w: cm.w];
Quaternion quatConjugate = [[Quaternion alloc] initWithValues:-cm.x y:-cm.y z:-cm.z w: cm.w];
[quat multiplyWithRight:e];
[quat multiplyWithRight:quatConjugate];
// quat.x, .y, .z contain your normal

Кватернион.h: 

@interface Quaternion : NSObject {
    double w;
    double x;
    double y;
    double z;
}

@property(readwrite, assign)double w;
@property(readwrite, assign)double x;
@property(readwrite, assign)double y;
@property(readwrite, assign)double z;

Кватернион.м: 

- (Quaternion*) multiplyWithRight:(Quaternion*)q {
    double newW = w*q.w - x*q.x - y*q.y - z*q.z;
    double newX = w*q.x + x*q.w + y*q.z - z*q.y;
    double newY = w*q.y + y*q.w + z*q.x - x*q.z;
    double newZ = w*q.z + z*q.w + x*q.y - y*q.x;
    w = newW;
    x = newX;
    y = newY;
    z = newZ;
    // one multiplication won't denormalise but when multipling again and again 
    // we should assure that the result is normalised
    return self;
}

- (id) initWithValues:(double)w2 x:(double)x2 y:(double)y2 z:(double)z2 {
        if ((self = [super init])) {
            x = x2; y = y2; z = z2; w = w2;
        }
        return self;
}

Я знаю, что кватернионы немного странны в начале, но как только вы есть идея, что они действительно гениальны. Это помогло мне представить кватернион как вращение вокруг вектора (x, y, z), а w-это (косинус) угла.

Если вам нужно сделать с ними больше, посмотрите на cocoamath open source project. Классы Quaternion и его расширение QuaternionOperations являются хорошей отправной точкой.

Для полноты картины, да, вы можете сделать это и с матричным умножением:

N = M * e

Но Я предпочел бы кватернионный способ, который избавляет вас от всех тригонометрических хлопот и работает лучше.

22

Спасибо Кей за отправную точку в решении. Вот моя реализация для всех, кто в ней нуждается. Я сделал пару небольших Щипков по совету Кей для моей ситуации. В качестве хедз-апа я использую только ландшафтную презентацию. У меня есть код, который обновляет переменную _isLandscapeLeft, чтобы сделать необходимую корректировку в направлении вектора.

Кватернион.h

    @interface Quaternion : NSObject{
    //double w;
    //double x;
    //double y;
    //double z;
}

@property(readwrite, assign)double w;
@property(readwrite, assign)double x;
@property(readwrite, assign)double y;
@property(readwrite, assign)double z;

- (id) initWithValues:(double)w2 x:(double)x2 y:(double)y2 z:(double)z2;
- (Quaternion*) multiplyWithRight:(Quaternion*)q;
@end

Кватернион.m

#import "Quaternion.h"

@implementation Quaternion


- (Quaternion*) multiplyWithRight:(Quaternion*)q {
    double newW = _w*q.w - _x*q.x - _y*q.y - _z*q.z;
    double newX = _w*q.x + _x*q.w + _y*q.z - _z*q.y;
    double newY = _w*q.y + _y*q.w + _z*q.x - _x*q.z;
    double newZ = _w*q.z + _z*q.w + _x*q.y - _y*q.x;
    _w = newW;
    _x = newX;
    _y = newY;
    _z = newZ;
    // one multiplication won't denormalise but when multipling again and again
    // we should assure that the result is normalised
    return self;
}

- (id) initWithValues:(double)w2 x:(double)x2 y:(double)y2 z:(double)z2 {
    if ((self = [super init])) {
        _x = x2; _y = y2; _z = z2; _w = w2;
    }
    return self;
}


@end

И мой игровой класс, который использует кватернион для стрельба: 

-(void)fireWeapon{
    ProjectileBaseClass *bullet = [[ProjectileBaseClass alloc] init];
    bullet.position = SCNVector3Make(0, 1, 0);
    [self.rootNode addChildNode:bullet];

    Quaternion *e = [[Quaternion alloc] initWithValues:0 x:0 y:0 z:1];
    CMQuaternion cm = _currentAttitude.quaternion;
    Quaternion *quat = [[Quaternion alloc] initWithValues:cm.w x:cm.x y:cm.y z:cm.z];
    Quaternion *quatConjugate = [[Quaternion alloc] initWithValues:cm.w x:-cm.x y:-cm.y z:-cm.z];
    quat = [quat multiplyWithRight:e];
    quat = [quat multiplyWithRight:quatConjugate];
    SCNVector3 directionToShoot;
    if (_isLandscapeLeft) {
        directionToShoot = SCNVector3Make(quat.y, -quat.x, -quat.z);

    }else{
        directionToShoot = SCNVector3Make(-quat.y, quat.x, -quat.z);

    }

    SCNAction *shootBullet = [SCNAction moveBy:directionToShoot duration:.1];
    [bullet runAction:[SCNAction repeatActionForever:shootBullet]];
}
3