Ориентация тетраэдра для треугольных сеток

У меня есть 2 треугольника и вершины p0, p1, p2, p3. Эти два треугольника имеют общее ребро. Из этих двух треугольников я хочу сделать тетраэдр, заданный 4 вершинами. Библиотека, с которой я работаю, требует, чтобы" 4 вершины были заданы таким образом, чтобы четыре вершины-тройки, определяющие грани тетраэдра на чертеже, появлялись в порядке против часовой стрелки при взгляде снаружи " 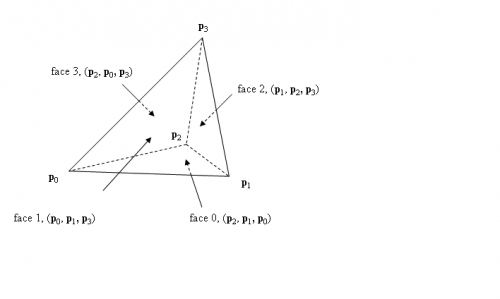рисунок . Предполагая, что один из двух треугольников равен p0, p1, p2, я вычисляю Нормаль как (p1-p0) (крест) (Р2-Р0). Может ли кто-нибудь, пожалуйста, сказать мне, как обеспечить выполнение этого условия ?

1 8
algorithm geometry computational-geometry

1 ответ:

Краткий ответ:

Условие состоит в том, что p3 должно находиться на правильной стороне плоскости, определяемой (p0, p1, p2).

Таким образом, после вычисления нормали для этой плоскости вам нужно определить, указывает ли вектор от (скажем) p0 до p3 в том же направлении нормали или в противоположном направлении, взяв точечное произведение dot(normal, p3-p0).

Говоря более математически:

Вам нужно найти определитель матрицы 4x4, образованной однородными координатами из четырех пунктов. Знак детерминанта определяет, выполняется ли условие; соответствующий знак зависит от используемых точных условностей, но в идеале он должен быть положительным: 

require:
  0 < det(p0, p1, p2, p3)

  == det [ p0.x p0.y p0.z 1 ]
         [ p1.x p1.y p1.z 1 ]
         [ p2.x p2.y p2.z 1 ]
         [ p3.x p3.y p3.z 1 ]

Если определенный упорядоченный набор точек имеет отрицательный детерминант, его можно исправить, поменяв местами любые две точки (что приведет к отрицанию детерминанта): 

e.g., swapping p0 and p2:

det(p0, p1, p2, p3) = - det(p2, p1, p0, p3)
     ^       ^               ^       ^

Или, в более общем смысле, переключение между четными и нечетными перестановками четырех вершин.

Если определитель равен ноль, четыре точки являются сопланарными и не могут быть зафиксированы подобным образом.

Наконец, код:

Относительно простой способ вычисления этого определителя с помощью трехмерной векторной математики: 

let:  v1 = p1 - p0
      v2 = p2 - p0
      v3 = p3 - p0
      norm12 = cross(v1, v2)
   -> determinant = dot(norm12, v3)
Конечный детерминант также известен как" тройное произведение " v1, v2 и v3. Обратите внимание, что я колебался, пытаясь расшифровать точную условность знака (то есть, нужно ли вам, чтобы определитель был положительным или отрицательным) из вашего вопроса: формулировка и диаграмма, которую вы предоставляете, являются более чем немного сбивает с толку. Однако, поскольку у вас есть оригинальная библиотека и ее документация, вы находитесь в лучшем положении, чтобы ответить на этот вопрос. В крайнем случае, вы можете попробовать эмпирический метод: попробуйте оба знака и выберите тот, который не взрывается...
12