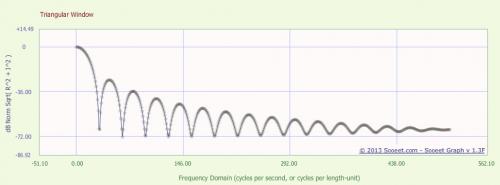
Окно Ханнинга и онлайн БПФ

Я изучаю DSP, и я не мог написать код для вычисления и построения этих цифр (просто величина Ханнинга и треугольных окон в частотной области.) Может кто-нибудь помочь мне с кодом?

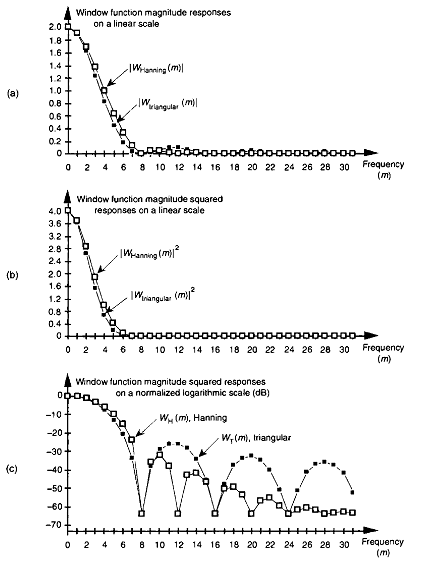
графики частоты окна

Я читал что-то, связанное с онлайн-БПФ, и, например, они вычисляют онлайн-БПФ с 1024 временными шагами. Я не понимаю, что такое 1024 временных шага и каково влияние значения временного шага на анализ БПФ?

3 3
matlab signal-processing fft

3 ответа:

Я надеюсь, что следующий фрагмент кода будет полезен для вас.

L = 10;
win1 = hanning(L);
win2 = triang(L);
nfft = 64;
S1 = fft(win1,nfft);
S2 = fft(win2,nfft);
f = 1:nfft/2+1;
plot(f,10*log10(abs(S1(1:nfft/2+1))),'.-',f,10*log10(abs(S2(1:nfft/2+1))),'o-');

Аннотация:

Вы можете поместить win1 и win2 в качестве сигнала временного ряда. L - длина win1 или win2. nfft - Длина БПФ . если L < nfft, то функция fft() добавит 0 к остальным nfft. Если L > nfft, то функция fft() перехватит длину L, равную nfft.

4

Частота временных шагов или выборок (Fs), деленная на число временных шагов, подаваемых в БПФ (длина БПФ), дает вам частотные шаги БПФ результирующих бункеров (до Fs/2).

1

Что касается 1024 "временных шагов" в вашем вопросе, то это просто число выборок, взятых из сигнала временной области.

Что касается того, как 1024 выборки во временной области влияют на БПФ, это включает частоту дискретизации, которая использовалась для получения выборок.

Частота дискретизации обычно выбирается в соответствии с теоремой Найквиста-Шеннона о дискретизации, которая в основном гласит, что вы должны дискретизировать сигнал во временной области на частоте выше, чем "2F", если вы хотите разрешите частоту " F " с помощью FFT.

Что касается кодов Ханна (Hanning) и треугольного окна, то они следующие: 

Hann window:
for( i=0; i<bufLen; i++ )
   window[i] = 0.5 * ( 1 - cos( 2 * PI * i / (bufLen-1) ) )

Triangular window:
for( i=0; i<bufLen; i++ )
   window[i] = 2/bufLen * ( (bufLen)/2 - abs( i-((bufLen-1)/2) ) )

...

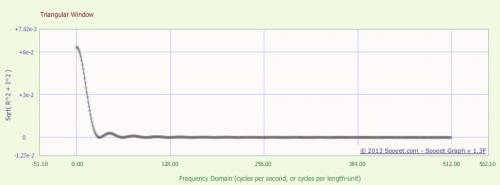
График ниже представляет собой частотную характеристику треугольного окна, выраженную в дБ.

Треугольная оконная функция величины дБ

График ниже представляет собой частотную характеристику треугольного окна, но теперь в линейной величине.

Треугольная функция окна линейная величина

Вы можете построить здесь функции окон Hann, Triangular и многие другие: построить окна функции

1