Насколько водонепроницаем швейцарский сыр? [закрытый]
Представьте себе кусочек швейцарского сыра в форме куба. Мы моделируем сыр через сетку 20x20x20. Для простоты мы предполагаем, что каждый куб сетки состоит полностью из сыра или полностью из воздуха. На верхнюю сторону нашего кубика швейцарского сыра мы затем наливаем воду, которая проникает в сыр только через воздушные отверстия в кубе. Вода может течь по непрерывному каналу сверху вниз, но она может течь только от одного воздушного куба к другому, если два куба соединены через лицо (не просто край или угол). Вода также может течь по обходным путям, например, в сливной ловушке раковины, но она не может вытекать на боковые стенки сырного кубика.
Теперь давайте программно реализуем эту модель швейцарского сыра со случайным распределением воздуха и кубиков сыра, как описано выше, с вероятностью сыра p и вероятностью воздуха 1 - p и смоделируем протекание воды через сыр, чтобы выяснить, протекает ли вода через сыр. до самого дна кубика швейцарского сыра. Многократно моделируя протекание воды через куб швейцарского сыра с различными вероятностями сыра и воздуха, мы можем установить связь между p и вероятностью протекания воды через дно Куба швейцарского сыра, назовем ее q . Результат выглядит так:q
1 ************************
0.8 *
0.6 *
0.4 *
0.2 *
0 ***********
0 0.2 0.4 0.6 0.8 1 p
Мой вопрос: Почему такая странная кривая?
Этот вопрос взят из 23-го федерального конкурс информатики в Германии (2004/2005) . Ответ на вопрос "почему такая странная кривая" не был представлен в интернете (решения предоставлены).
Я надеюсь, что я в правильном месте с такого рода вопросом.
2 ответа:
Возможно, вы найдете следующее объяснение интуитивно понятным:
В вашем случае, 20*20*20 клетки, если у вас нет хотя бы 20 отверстий, вероятность потока воды равна ровно 0. Если у вас есть 20 отверстий, вода может течь, если вы упорядочите их в колонне, но вероятность того, что такой порядок появляется случайным образом, очень мала, 20*20/гребень(20^3, 20) ~= 1e-57. По мере того как вы увеличиваете число отверстий, появление смежных путей становится все более и более вероятным.
Когда все ваши клетки, кроме 20*20 из них есть отверстия, единственный способ блокировать поток-это упорядочить все ячейки сыра в один "блокирующий" слой, например горизонтальный слой 20*20. (Есть и другие возможные конфигурации, но не слишком вероятные. Вам нужен ровно один сырный блок для каждой (x, y) координаты, и каждый сырный блок должен быть в контакте со всеми своими (x, y)-соседями. Но они могут быть распределены вдоль оси z).
Если у вас меньше 20 * 20 сырных блоков, вы не можете сформировать полный слой и вероятность потока будет ровно 1.
Это продолжение комментария Жени.
Как уже упоминалось, ваш швейцарский сыр является примеромтеории перколяции . Это фундаментальное понятие статистической механики, когда мы рассматриваем предмет фазовых переходов. Один из канонических примеров теории перколяции очень похож на вопрос, который вы опубликовали.Модель Эрдеша–Рени
В модели Erdős-Rényi вы начинаете с пустого графа и соедините узлы ребром с вероятностью
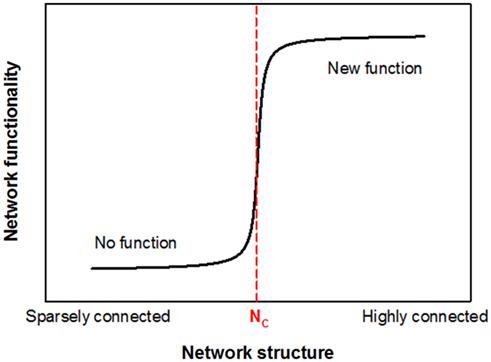
p. При некотором критическом значенииpструктура графа изменяется от связки несвязанных кластеров до одной большой связующей структуры, содержащей большую долю узлов. На самом деле, если бы вы построили график среднего размера самого большого кластера, вы получили бы очень похожую картину, как ваша модель швейцарского сыра! Схематически это выглядит так:
И вы найдете его в многих примерах в прикладной математика и физика. Заслуга картины исходит из этой статьи в Frontiers, где обсуждаются эти явления гораздо более подробно.