Нахождение кратчайшего пути в графе, который посещает X узлов по крайней мере один раз
Несмотря на то, что я все еще новичок, я люблю решать задачи, связанные с графами (кратчайший путь, поиск и т. д.). Недавно я столкнулся с такой проблемой:
Учитывая неориентированный, взвешенный (без отрицательных значений) граф с N узлами и E ребрами (максимум 1 ребро между двумя узлами, ребро может быть помещено только между двумя различными узлами) и список X узлов, которые вы должны посетить, найдите кратчайший путь, который начинается с узла 0, посещает все X узлов и возвращается к узлу 0. Там всегда есть по крайней мере, один путь, соединяющий любые два узла.
Пределы равны 1
Вот пример:
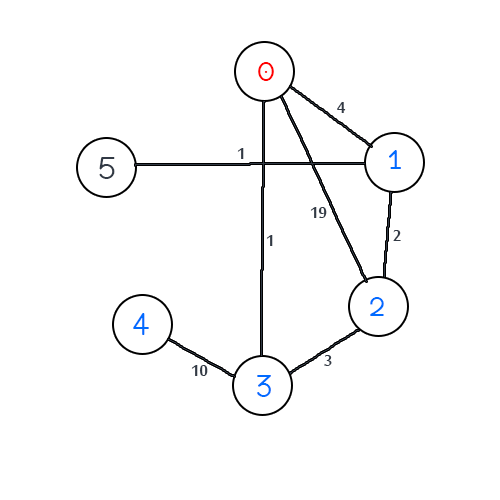
0 -> 3 -> 4 -> 3 -> 2 -> 1 -> 0 с общей стоимостью 30
Я думал об использовании Дейкстры, чтобы найти кратчайший путь между всеми X (синие) узлы, а затем просто жадно выбирает ближайший не посещенный X (синий) узел, но это не работает (приходит с 32 вместо 30 на бумаге). Кроме того, позже я заметил, что просто нахождение кратчайшего пути между всеми парами X узлов займет O(X*N^2) времени, которое слишком велико с таким количеством узлов.
Единственное, что я смог найти для схем, - это Эйлерова схема, которая позволяет посещать каждый узел только один раз (и мне это не нужно). Можно ли это решить с помощью Дейкстры или есть какой-либо другой алгоритм, который можно ли это решить?1 ответ:
Вот решение, которое, вероятно, будет достаточно быстрым:
1) запустить алгоритм поиска кратчайшего пути из каждого синего узла(это можно сделать в O (X * (E log N))) для вычисления попарных расстояний.
2) построить новый граф с нулевой вершиной и только синими вершинами (X + 1 вершина). Добавьте ребра, используя попарные расстояния, вычисленные на первом шаге.
3) новый граф достаточно мал, чтобы использовать решение динамического программирования для TSP(он имеет временную сложность O (X^2 * 2^X)).