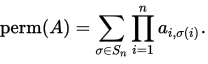Может ли этот код cython быть оптимизирован?
Я впервые использую cython, чтобы получить некоторую скорость для функции. Функция принимает квадратную матрицу A чисел с плавающей запятой и выводит одно число с плавающей запятой. Вычисляемая функция является перманентом матрицы
Когда A равно 30 на 30, мой код занимает около 60 секунд на моем компьютере.
В приведенном ниже коде я реализовал формулу Баласубраманьяна-бакса / Франклина-Глинна для перманента из Вики страница. Я назвал матрицу M.
Одной из сложных частей кода является массив f, который используется для хранения индекса следующей позиции для переворота в массиве d. массив d содержит значения, которые равны +-1. Манипуляции с f и j в цикле - это просто умный способ быстро обновить серый код.
from __future__ import division
import numpy as np
cimport numpy as np
cimport cython
DTYPE_int = np.int
ctypedef np.int_t DTYPE_int_t
DTYPE_float = np.float64
ctypedef np.float64_t DTYPE_float_t
@cython.boundscheck(False) # turn off bounds-checking for entire function
@cython.wraparound(False) # turn off negative index wrapping for entire function
def permfunc(np.ndarray [DTYPE_float_t, ndim =2, mode='c'] M):
cdef int n = M.shape[0]
cdef np.ndarray[DTYPE_float_t, ndim =1, mode='c' ] d = np.ones(n, dtype=DTYPE_float)
cdef int j = 0
cdef int s = 1
cdef np.ndarray [DTYPE_int_t, ndim =1, mode='c'] f = np.arange(n, dtype=DTYPE_int)
cdef np.ndarray [DTYPE_float_t, ndim =1, mode='c'] v = M.sum(axis=0)
cdef DTYPE_float_t p = 1
cdef int i
cdef DTYPE_float_t prod
for i in range(n):
p *= v[i]
while (j < n-1):
for i in range(n):
v[i] -= 2*d[j]*M[j, i]
d[j] = -d[j]
s = -s
prod = 1
for i in range(n):
prod *= v[i]
p += s*prod
f[0] = 0
f[j] = f[j+1]
f[j+1] = j+1
j = f[0]
return p/2**(n-1)
Я использовал все простые оптимизации, которые я нашел в учебнике cython. Некоторые аспекты, которые я должен признать, я не совсем понимаю. Например, если я сделаю массив d ints, поскольку значения всегда только +-1, код выполняется примерно на 10% медленнее, поэтому я оставил его как float64s.
Есть ли что-нибудь еще, что я могу сделать, чтобы ускорить код?
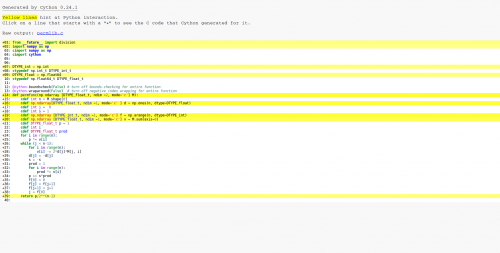
Это результат действия цитона-А. Как вы можете видеть, все в цикле скомпилировано на C, поэтому основные оптимизации сработали.
Здесь та же функция в numpy, которая более чем в 100 раз медленнее, чем мой текущий цитон версия.
def npperm(M):
n = M.shape[0]
d = np.ones(n)
j = 0
s = 1
f = np.arange(n)
v = M.sum(axis=0)
p = np.prod(v)
while (j < n-1):
v -= 2*d[j]*M[j]
d[j] = -d[j]
s = -s
prod = np.prod(v)
p += s*prod
f[0] = 0
f[j] = f[j+1]
f[j+1] = j+1
j = f[0]
return p/2**(n-1)
Обновленные тайминги
Вот тайминги (с использованием ipython) моей версии cython, версии numpy и улучшения romeric в коде cython. Я установил семя для воспроизводимости.
from scipy.stats import ortho_group
import pyximport; pyximport.install()
import permlib # This loads in the functions from permlib.pyx
import numpy as np; np.random.seed(7)
M = ortho_group.rvs(23) #Creates a random orthogonal matrix
%timeit permlib.npperm(M) # The numpy version
1 loop, best of 3: 44.5 s per loop
%timeit permlib.permfunc(M) # The cython version
1 loop, best of 3: 273 ms per loop
%timeit permlib.permfunc_modified(M) #romeric's improvement
10 loops, best of 3: 198 ms per loop
M = ortho_group.rvs(28)
%timeit permlib.permfunc(M) # The cython version run on a 28x28 matrix
1 loop, best of 3: 15.8 s per loop
%timeit permlib.permfunc_modified(M) # romeric's improvement run on a 28x28 matrix
1 loop, best of 3: 12.4 s per loop
Можно ли вообще ускорить код цитона?
Я использую gcc, а процессор-AMD FX 8350.
4 ответа:
Этот ответ основан на коде @romeric, опубликованном ранее. Я исправил код, упростил его и добавил директиву компилятора
cdivision.@cython.boundscheck(False) @cython.wraparound(False) @cython.cdivision(True) def permfunc_modified_2(np.ndarray [double, ndim =2, mode='c'] M): cdef: int n = M.shape[0], s=1, i, j int *f = <int*>malloc(n*sizeof(int)) double *d = <double*>malloc(n*sizeof(double)) double *v = <double*>malloc(n*sizeof(double)) double p = 1, prod for i in range(n): v[i] = 0. for j in range(n): v[i] += M[j,i] p *= v[i] f[i] = i d[i] = 1 j = 0 while (j < n-1): prod = 1. for i in range(n): v[i] -= 2.*d[j]*M[j, i] prod *= v[i] d[j] = -d[j] s = -s p += s*prod f[0] = 0 f[j] = f[j+1] f[j+1] = j+1 j = f[0] free(d) free(f) free(v) return p/pow(2.,(n-1))Исходный код @romeric не инициализировал
v, поэтому иногда вы получаете разные результаты. Кроме того, я объединил две петли передwhileи две петли внутриwhileсоответственно.Наконец, сравнение
In [1]: from scipy.stats import ortho_group In [2]: import permlib In [3]: import numpy as np; np.random.seed(7) In [4]: M = ortho_group.rvs(5) In [5]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M)) Out[5]: True In [6]: %timeit permfunc(M) 10000 loops, best of 3: 20.5 µs per loop In [7]: %timeit permlib.permfunc_modified_2(M) 1000000 loops, best of 3: 1.21 µs per loop In [8]: M = ortho_group.rvs(15) In [9]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M)) Out[9]: True In [10]: %timeit permlib.permfunc(M) 1000 loops, best of 3: 1.03 ms per loop In [11]: %timeit permlib.permfunc_modified_2(M) 1000 loops, best of 3: 432 µs per loop In [12]: M = ortho_group.rvs(28) In [13]: np.equal(permlib.permfunc(M), permlib.permfunc_modified_2(M)) Out[13]: True In [14]: %timeit permlib.permfunc(M) 1 loop, best of 3: 14 s per loop In [15]: %timeit permlib.permfunc_modified_2(M) 1 loop, best of 3: 5.73 s per loop
Вы мало что можете сделать со своей функцией
cython, так как она уже хорошо оптимизирована. Тем не менее, вы все равно сможете получить умеренное ускорение, полностью избегая вызововnumpy.import numpy as np cimport numpy as np cimport cython from libc.stdlib cimport malloc, free from libc.math cimport pow cdef inline double sum_axis(double *v, double *M, int n): cdef: int i, j for i in range(n): for j in range(n): v[i] += M[j*n+i] @cython.boundscheck(False) @cython.wraparound(False) def permfunc_modified(np.ndarray [double, ndim =2, mode='c'] M): cdef: int n = M.shape[0], j=0, s=1, i int *f = <int*>malloc(n*sizeof(int)) double *d = <double*>malloc(n*sizeof(double)) double *v = <double*>malloc(n*sizeof(double)) double p = 1, prod sum_axis(v,&M[0,0],n) for i in range(n): p *= v[i] f[i] = i d[i] = 1 while (j < n-1): for i in range(n): v[i] -= 2.*d[j]*M[j, i] d[j] = -d[j] s = -s prod = 1 for i in range(n): prod *= v[i] p += s*prod f[0] = 0 f[j] = f[j+1] f[j+1] = j+1 j = f[0] free(d) free(f) free(v) return p/pow(2.,(n-1))Вот основные проверки и тайминги:
In [1]: n = 12 In [2]: M = np.random.rand(n,n) In [3]: np.allclose(permfunc_modified(M),permfunc(M)) True In [4]: n = 28 In [5]: M = np.random.rand(n,n) In [6]: %timeit permfunc(M) # your version 1 loop, best of 3: 28.9 s per loop In [7]: %timeit permfunc_modified(M) # modified version posted above 1 loop, best of 3: 21.4 s per loopEDIT Давайте выполним некоторую базовую векторизацию
SSE, развернув внутренний циклprod, то есть изменим цикл в приведенном выше коде на следующий# define t1, t2 and t3 earlier as doubles t1,t2,t3=1.,1.,1. for i in range(0,n-1,2): t1 *= v[i] t2 *= v[i+1] # define k earlier as int for k in range(i+2,n): t3 *= v[k] p += s*(t1*t2*t3)А теперь время
In [8]: %timeit permfunc_modified_vec(M) # vectorised 1 loop, best of 3: 14.0 s per loopТак что почти 2X ускорение по сравнению с исходным оптимизированным кодом cython, неплохо.
отказ от ответственности: я основной разработчик инструмента, упомянутого ниже.
В качестве альтернативы на Cython, вы можете дать Pythran попробовать. Одной аннотации в исходный код включает в себя:
#pythran export npperm(float[:, :]) import numpy as np def npperm(M): n = M.shape[0] d = np.ones(n) j = 0 s = 1 f = np.arange(n) v = M.sum(axis=0) p = np.prod(v) while j < n-1: v -= 2*d[j]*M[j] d[j] = -d[j] s = -s prod = np.prod(v) p += s*prod f[0] = 0 f[j] = f[j+1] f[j+1] = j+1 j = f[0] return p/2**(n-1)Скомпилировано с:
> pythran perm.pyДает ускорение, аналогичное тому, которое имеет Cython:
> # numpy version > python -mtimeit -r3 -n1 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)' 1 loops, best of 3: 21.7 sec per loop > # pythran version > pythran perm.py > python -mtimeit -r3 -n1 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)' 1 loops, best of 3: 171 msec per loopБез необходимости переосмысления
sum_axis(Об этом заботится Пифран).Что еще интереснее, Пифран способен распознавать несколько векторизуемых (в смысле порождающих SSE / AVX intrinsics) паттерны, через флаг опции:
> pythran perm.py -DUSE_BOOST_SIMD -march=native > python -mtimeit -r3 -n10 -s 'from scipy.stats import ortho_group; from perm import npperm; import numpy as np; np.random.seed(7); M = ortho_group.rvs(23)' 'npperm(M)' 10 loops, best of 3: 93.2 msec per loopЧто делает окончательное ускорение x232 по отношению к версии NumPy, ускорение, сравнимое с развернутой версией Cython, без большой ручной настройки.
Ну, одна очевидная оптимизация состоит в том, чтобы установить d[i] в -2 и +2 и избежать умножения на 2. Я подозреваю, что это ничего не изменит, но все же.
Другой способ - убедиться, что компилятор C++, который компилирует результирующий код, включает все оптимизации (особенно векторизацию).
Цикл, который вычисляет новый v[i]s, может быть распараллелен с поддержкойCython OpenMP . При 30 итерациях это также может не иметь значения.