Могут ли панды найти все линии, которые соединяют любую пару * * точек* *и не пересекают ни одну из заданных ** линий* * без итерации?
Задан правильно определенный список точек и список строк:
Могут ли панды найти все линии, которые соединяют любую пару точек и не пересекают ни одну из заданных линий без итерации?В настоящее время я добираюсь до решения, как вы можете видеть на изображении, но я должен повторить процесс, и эта итерация делает все мучительно медленным.
На изображении список точек - это нарисованные цветные точки, А список линии будут свечами. Желаемый результат-это черные линии.
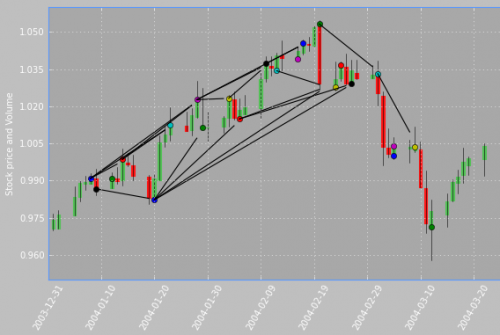
Хотя вопрос нацелен на теоретическое решение или концептуальное подтверждение, если это возможно или нет другого способа, кроме итераций, вот код, который я сейчас использую, если это поможет: http://pastebin.com/4DiKVy26
1 ответ:
Я не знаю панд, но я вижу, что вы пытаетесь сделать, и да, это можно сделать быстрее. Я буду называть черные линии лучами по причинам, которые, я надеюсь, станут ясными; в вашем алгоритме, с m точками и n линиями, вы находите все M(m-1)/2 луча, а затем делаете 2n сравнений, чтобы отфильтровать их: m*(m-1)*n => кубический размер входного сигнала. Есть способ сделать это квадратичным на входе.
То, что вы описываете, можно решить с помощью формы райкастинг (хотя проще, потому что это в 2d): думайте о точках как о огнях; исходная точка может только отбрасывать луч на целевую точку, если цель не находится в тени линии. Итак, мы начинаем с точки и перемещаемся вправо по списку линий и точек, которые вы можете осветить. Когда мы проходим мимо линий, будет расширяться область тени; но при любом значении x нам нужно только знать 2 градиента края тени, чтобы знать, находится ли значение y в тени. Как мы проходим каждую линию идя направо, обновите градиенты тени. Проходя мимо каждой точки, мы проверяем, лежит ли она вне тени; если да, то у нас есть луч. Повторите этот процесс для каждой точки, и вы закончите. Это работает примерно как M*(m-1)/2+m * n вычислений, которые масштабируются намного лучше.