Маска кругового сектора в массиве numpy

У меня есть код, который разрезает массив numpy на окружности. Я хочу восстановить только значения, включенные в определенный диапазон углов из окружности, и замаскировать массив. Например: маскируйте исходный массив позициями (x, y), расположенными между 0 и 45 градусами окружности.

Есть ли для этого какой-то питонский способ?

Вот мой (упрощенный) исходный код: 

import numpy as np
matrix = np.zeros((500,500))
x = 240
y = 280
radius = 10
mask=np.ogrid[x-radius:x+radius+1,y-radius:y+radius+1]
matrix[mask]

Заранее спасибо

Edit: я опустил, что радиус может изменяться.

2 9
python numpy angle matrix

2 ответа:

Я бы сделал это путем преобразования декартовых координат в полярные и построения булевых масок для круга и для диапазона углов, которые вы хотите:

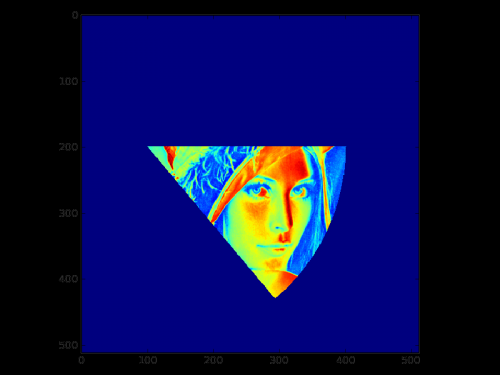
import numpy as np

def sector_mask(shape,centre,radius,angle_range):
    """
    Return a boolean mask for a circular sector. The start/stop angles in  
    `angle_range` should be given in clockwise order.
    """

    x,y = np.ogrid[:shape[0],:shape[1]]
    cx,cy = centre
    tmin,tmax = np.deg2rad(angle_range)

    # ensure stop angle > start angle
    if tmax < tmin:
            tmax += 2*np.pi

    # convert cartesian --> polar coordinates
    r2 = (x-cx)*(x-cx) + (y-cy)*(y-cy)
    theta = np.arctan2(x-cx,y-cy) - tmin

    # wrap angles between 0 and 2*pi
    theta %= (2*np.pi)

    # circular mask
    circmask = r2 <= radius*radius

    # angular mask
    anglemask = theta <= (tmax-tmin)

    return circmask*anglemask

Например: 

from matplotlib import pyplot as pp
from scipy.misc import lena

matrix = lena()
mask = sector_mask(matrix.shape,(200,100),300,(0,50))
matrix[~mask] = 0
pp.imshow(matrix)
pp.show()

Введите описание изображения здесь

18

Тот же подход для центрированных кругов в квадратных матрицах: 

def circleMask(mat, r=0):
    if mat.shape[0] != mat.shape[1]:
        raise TypeError('Matrix has to be square')
    if not isinstance(r, int):
        raise TypeError('Radius has to be of type int')

    s = mat.shape[0]
    d = num.abs(num.arange(-s/2 + s%2, s/2 + s%2))
    dm = num.sqrt(d[:, num.newaxis]**2 + d[num.newaxis, :]**2)

    return num.logical_and(dm >= r-.5, dm < r+.5)

Цикл над этой неявной функцией является дорогостоящим!

1