Линейная регрессия с pymc3 и убеждением

Я пытаюсь понять статистику Байесайна с помощью pymc3

Я запустил этот код для простой линейной регрессии 

#Generating data y=a+bx
import pymc3
import numpy as np
N=1000
alpha,beta, sigma = 2.0, 0.5, 1.0
np.random.seed(47)
X = np.linspace(0, 1, N)
Y = alpha + beta*X + np.random.randn(N)*sigma

#Fitting
linear_model = pymc3.Model()
with linear_model:
    alpha = pymc3.Normal('alpha', mu=0, sd=10)
    beta = pymc3.Normal('beta', mu=0, sd=10)
    sigma = pymc3.HalfNormal('sigma', sd=1)
    mu = alpha + beta*X
    Y_obs = pymc3.Normal('Y_obs', mu=mu, sd=sigma, observed=Y)

    start = pymc3.find_MAP(fmin=optimize.fmin_powell)
    step = pymc3.NUTS(scaling=start)
    trace = pymc3.sample(500, step, start=start)

Я не понимаю, что означает след

Если я достаточно хорошо понимаю байесовскую теорию, то должна существовать функция belief, которая получает alpha,beta и sigma и выводит вероятность их сочетания.

Как я могу получить эту belief структуру из переменных trace?

1 4
python bayesian

1 ответ:

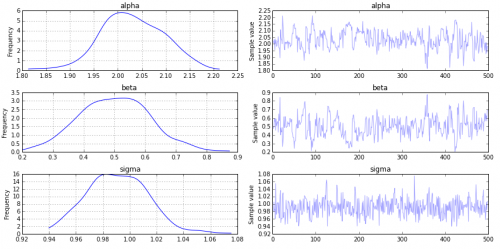
trace является результатом процесса Монте-Карло Марковской цепи (MCMC). Он сходится к распределению (например, убеждению) ваших параметров, учитывая данные.

Вы можете просмотреть трассировку, используя:

pymc3.traceplot(trace, vars=['alpha', 'beta', 'sigma'])

Проследить Сюжет

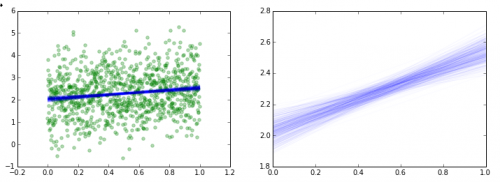
Если вы хотите увидеть индивидуальные реализации вашей регрессии вдоль каждой точки следа, вы можете сделать что-то вроде этого: 

import matplotlib.pyplot as plt

a = trace['alpha']
b = trace['beta']
x = np.linspace(0,1,N)

fig = plt.figure(figsize=(12,4))

ax = fig.add_subplot(1,2,1)
plt.scatter(X,Y, color='g', alpha=0.3)
for i in xrange(500):
  y = a[i] + b[i] * x
  plt.plot(x, y, 'b', alpha=0.02)

ax = fig.add_subplot(1,2,2)
for i in xrange(500):
  y = a[i] + b[i] * x
  plt.plot(x, y, 'b', alpha=0.02)
plt.show()

Индивидуальные Реализации

Примечание : похоже, что в вашем коде отсутствует строка: from scipy import optimize

8