Коммивояжер (нужно посетить только подмножество узлов): прослушивается

Мне нужна помощь с моим кодом проблемы коммивояжера. Его прослушивали... Я знаю, потому что это школьное задание и есть тестовые случаи. Ну вот и все.

Задан связный граф, в котором мне нужно посетить подмножество узлов. Как вычислить кратчайший путь?

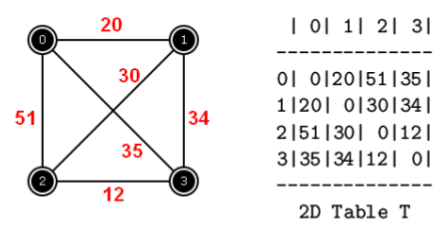
В качестве примера обратитесь к приведенному выше изображению. Мне нужно начать с 0 и посетить некоторые / все узлы, а затем вернуться к нулю. В процессе мне нужно вычислить кратчайший путь.

Предположим, мне нужно чтобы посетить все узлы, я буду идти от 0 -> 1 -> 2 -> 3 -> 0 = 20 + 30 + 12 + 35 = 97. Предположим, что теперь мне нужно только посетить узел 2, я пойду от 0 -> 3 -> 2 -> 3 -> 0, поскольку это дает кратчайший путь 94 (я могу посетить узлы, которые мне не нужно посещать, если он может дать кратчайший путь).

В основном, я сделал:

1. Вычислите кратчайший путь между любыми 2 парами требуемых узлов и источником (0). Это дает мне кратчайший путь 2D-таблицы, как (я использовал dijkstra):

     |  0  1  2  3
   --+--------------
   0 | 
   1 |
   2 | 
   3 |
   

2. Теперь я модифицирую продавца покупок алгоритм (он же. Флойд Warshall или АПСП), чтобы использовать эту таблицу. Текущий источник Java (TSP и dijkstra) выглядит следующим образом:

   int TSP(int source, int visited) {
      if (visited == (int)(Math.pow(2, K)-1)) { // all required visited
       return sssp.get(source).get(0); // return to source (0)
     } else if (memo.containsKey(source) && memo.get(source).containsKey(visited)) {
       return memo.get(source).get(visited);
     } else {
       int item;
       if (!memo.containsKey(source)) {
         memo.put(source, new HashMap<Integer, Integer>());
       }
       memo.get(source).put(visited, 1000000);
       for (int v = 0; v < K; v++) {
         item = shoppingList[v];
         if (!hasVisited(visited, item)) {
           memo.get(source).put(visited, Math.min(
             memo.get(source).get(visited),
             sssp.get(source).get(item) + TSP(item, visit(visited, v))
           ));
         }
       }
       return memo.get(source).get(visited);
     }
   }
   
   int dijkstra(int src, int dest) {
     PriorityQueue<IntegerPair> PQ = new PriorityQueue<IntegerPair>();
     HashMap<Integer, Integer> dist = new HashMap<Integer, Integer>(); // shortest known dist from {src} to {node}
     // init shortest known distance
     for (int i = 0; i < N+1; i++) {
       if (i != src) {
         dist.put(i, Integer.MAX_VALUE); // dist to any {i} is big(unknown) by default
       } else {
         dist.put(src, 0); // dist to {src} is always 0
       }
     }
     IntegerPair node;
     int nodeDist;
     int nodeIndex;
   
     PQ.offer(new IntegerPair(0, src)); 
     while (PQ.size() > 0) {
       node = PQ.poll();
       nodeDist = node.first();
       nodeIndex = node.second();
   
       if (nodeDist == dist.get(nodeIndex)) {
         // process out going edges
         for (int v = 0; v < N+1; v++) { // since its a complete graph, process all edges
           if (v != nodeIndex) { // except curr node
             if (dist.get(v) > dist.get(nodeIndex) + T[nodeIndex][v]) { // relax if possible
               dist.put(v, dist.get(nodeIndex) + T[nodeIndex][v]);
               PQ.offer(new IntegerPair(dist.get(v), v));
             }
           }
         }
       }
     }
     return dist.get(dest);
   }
   

   1. visited используется в качестве битовой маски для указания, посещен ли узел
   2. sssp - это HashMap<Integer, HashMap<Integer, Integer>>, где ключ 1-й хэшмапы является исходным узлом, а ключ 2-й хэшмапы-конечным. Таким образом, он в основном представляет собой 2D-таблицу, которую вы видите в пункте 1.
   3. memo - это как раз то, что я использовал в динамическом программировании в качестве "кэша" ранее вычисленных кратчайший путь от узла, заданного посещаемым растровым изображением.

Полный источник: http://pastie.org/5171509

Тестовый случай, который проходит:

1

3 3
1 2 3
0 20 51 35
20 0 30 34
51 30 0 12  
35 34 12 0 

Где 1-я строка-количество тестовых случаев. 3-я строка (3 3). 1-й 3 - это число узлов, 2-й 3-это число требуемых узлов. 4-я строка-это список необходимых узлов. Далее следует таблица Весов ребер.

Тестовый случай, который терпит неудачу, является:

9 9
1 2 3 4 5 6 7 8 9
0 42 360 335 188 170 725 479 359 206
42 0 402 377 146 212 767 521 401 248
360 402 0 573 548 190 392 488 490 154
335 377 573 0 293 383 422 717 683 419
188 146 548 293 0 358 715 667 539 394
170 212 190 383 358 0 582 370 300 36
725 767 392 422 715 582 0 880 704 546
479 521 488 717 667 370 880 0 323 334
359 401 490 683 539 300 704 323 0 336
206 248 154 419 394 36 546 334 336 0

Я получил 3995, но ответ-2537... извините, я знаю, что это трудно отладить ... У меня та же проблема, тестовый случай слишком велик ... по крайней мере, для людей ... поэтому я создаю меньший тестовый случай, чтобы проверить ,но они, кажется, проходят...