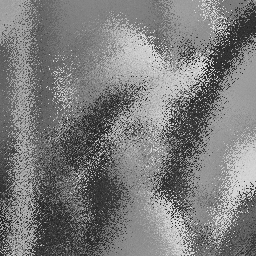Как вы используете шум питона 1.1.1 для координат?

Я огляделся и, кажется, больше всего использую его для текстур, и я застрял, пытаясь понять, как реализовать шум Perlin / Simplex для набора 2-мерных координат x и y.

Все, что я пытаюсь сделать, это ввести 2 случайные координаты, x & y, а затем он возвращает измененное x & y, или это невозможно?

Я использую pythons noise, чтобы создать координаты, но я обнаружил, что шум Перлина довольно сложен для понимания и не может полностью поймите, как это работает.

1 2
python perlin-noise

1 ответ:

Можно использовать шум Перлина для добавления некоторой неопределенности к коллекции двумерных координат (если коллекция представляет собой одну пару, это тоже хорошо). Вы можете рассмотреть возвращаемое значение шума (в диапазоне [-1, 1] для указанной библиотеки) вместе с некоторым фактором, чтобы определить, насколько он влияет на ваши входные координаты. Чем больше коэффициент, тем большее влияние шум оказывает на ваши данные. Вот один из самых простых возможных примеров: 

from noise import snoise2 # Simplex noise for 2D points

x, y = 0.5, 0.3
factor = 0.1
n = snoise2(x, y)
print x + n * factor, y + n * factor

Мы также можем рассмотреть много более крупный фактор и применить ту же идею к изображениям. Рассматривая factor = 15 и округляя полученные координаты до ближайшего соседа, переходим от изображения слева к изображению справа:

Введите описание изображения здесьВведите описание изображения здесь

Полный код для получения изображения приведен ниже. Коэффициенты n1 и n2 использовались для получения "менее скучного" изображения. 
import sys
from noise import snoise2
from PIL import Image

img = Image.open(sys.argv[1]).convert('L')
result = Image.new('L', img.size)
width, height = img.size

factor = 15
res = result.load()
im = img.load()
for x in xrange(width):
    for y in xrange(height):
        n1 = snoise2(x, y)
        n2 = snoise2(y, x)
        pt = [int(round(x + n1 * factor)), int(round(y + n2 * factor))]
        pt[0] = min(max(0, pt[0]), width - 1)
        pt[1] = min(max(0, pt[1]), height - 1)
        res[x, y] = im[tuple(pt)]
result.save(sys.argv[2])
Конечно, это даже не царапает, как можно использовать шум Перлина. В качестве другого примера, учитывая определенную функцию, вы можете "зашумить" входы и комбинировать с указанным фактором для создания различных выходов. Например, вот результат выполнения этого на некоторой функции, основанной на косинусе:

Введите описание изображения здесь

2