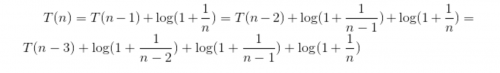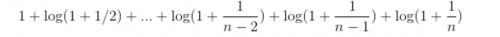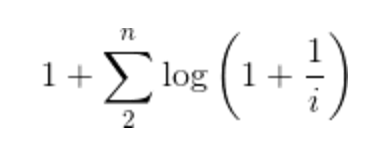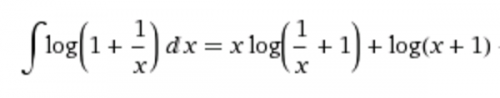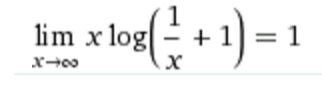Как решить для этого рекуррента T (n) = T(n - 1) + lg(1 + 1/n), T(1) = 1?
Я застрял в этом повторении:
T(n) = T(n − 1) + lg(1 + 1/n), T(1) = 1?
Некоторое время, и кажется, что главный метод не может быть применен к этому.
3 ответа:
У нас есть:
lg(1 + 1/n) = lg((n + 1) / n) = lg(n+1) - lg(n)Отсюда:
T(n) - T(n - 1) = lg(n + 1) - lg(n)
T(n-1) - T(n - 2) = lg(n) - lg(n - 1)
...
T(3) - T(2) = lg(3) - lg(2)
T(2) - T(1) = lg(2) - lg(1)Добавляя и устраняя, получаем:
T(n) - T(1) = lg(n + 1) - lg(1) = lg(n + 1)Или
T(n) = 1 + lg(n + 1)Отсюда
T(n) = O(lg(n))
Такой же ответ, как и другой правильный ответ здесь, только доказанный по-другому.
Из заданной рекурренции создаются все следующие уравнения:
- T (n) = T(n-1) + Log ((n+1)/n)
- T (n-1) = T(n-2) + Log (n/(n-1))
- .
- .
- .
- T (2) = T (1) + Log (3/2)
Суммирование всех RHS и LHS в приведенных выше уравнениях приводит к:
- T (n) = T(1) + Log(3/2) + Log(4/3)+... + Log ((n+1)/n)
Так как Log (a) + Log (b) = Log (ab),
- T (n) = 1 + Log ((n+1)/2)
- T (n) = Log (10) + Log ((n+1)/2) = Log (5n + 5) предполагая, что база равна 10 и используя 1 = Log1010
Поэтому T(n) = O (Log(5n + 5)) = O (Log (n))
Это не линейно, как утверждают некоторые люди. Это
O(log(n)). Вот математический анализ:
Если вы начнете разворачивать рекурсию, то получите:
Если вы будете делать это до конца, у вас будет
Или в краткой форме:
Как только вы приблизите сумму с помощью интеграла, вы получите:
Наконец, если вы возьмете предел x - > бесконечность:
Вы увидите, что первая часть является
, что дает вам окончательное решение
log(x + 1), которое являетсяO(log(n))