Как рассчитать начальную скорость движения снаряда на заданное расстояние и угол от точки А до точки в?
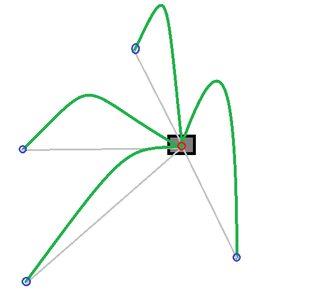
Пример изображения (Этот график не точен, но идея или парабола как там)
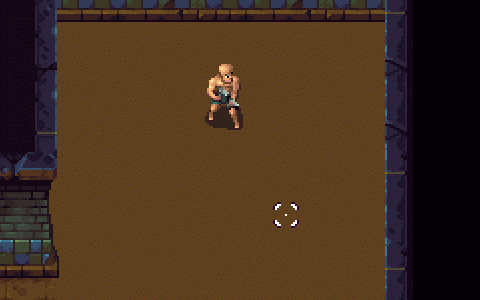
На приведенном ниже изображении зеленая криволинейная линия является движением снаряда пули, серая линия-движением тени, красный круг-начальным положением, а синий круг-местом назначения. В настоящее время я могу добиться движения тени, но, к сожалению, движение снаряда не так правильно, как на втором изображении ниже. Пожалуйста, смотрите ссылку Вот как я в данный момент двигаем пулю.Пример GIF (именно такого результата я и хотел!)
В приведенном ниже GIF, когда пуля выпущена, пуля имеет движение снаряда и все еще движется к центральной точке перекрестия.
Чтобы переместить пулю к месту назначения
В приведенном ниже коде описан способ перемещения пули к месту назначения с постоянной заданной скоростью 6 метров. Иметь возможность для достижения указанной выше траектории изображения мне нужно рассчитать скорость на заданном расстоянии.float bulletSpeed = 6; // In the mean time the speed is constant, but this should be calculated base on distance and angle
Vector2 touchPoint = new Vector2(input.touchpoint.x, input.touchpoint.y);
Vector2 targetDirection = touchPoint.cpy().sub(bulletPosition).nor();
Vector2 targetVelocity = targetDirection.cpy().scl(bulletSpeed);
float targetAngle = targetDirection.angle();
float targetDistance = touchPoint.dst(bulletPosition);
body.setLinearVelocity(targetVelocity);
Нарисовать проецируемую траекторию
Здесь нет никаких проблем, это основано напримере проекции траектории iforce2d .
startingPosition.set(originPoint); // Bullet Position
startingVelocity.set(targetDirection); // Calculated target direction
shape.setProjectionMatrix(CameraManager.getInstance().getCamera().combined);
shape.begin(ShapeRenderer.ShapeType.Point);
for (int i = 0; i < 180; i++) { // three seconds at 60fps
Vector2 trajectoryPosition = getTrajectoryPoint(startingPosition, startingVelocity, i);
shape.point(trajectoryPosition.x, trajectoryPosition.y, 0);
}
shape.end();
Получение точки траектории
public Vector2 getTrajectoryPoint(Vector2 startingPosition, Vector2 startingVelocity, float n) {
Vector2 gravity = WorldManager.getWorld().getGravity();
float t = 1 / 60.0f; // seconds per time step (at 60fps)
Vector2 stepVelocity = startingVelocity.cpy().scl(t); // m/s
Vector2 stepGravity = gravity.cpy().scl(t * t); // m/s/s
Vector2 trajectoryPoint = new Vector2();
trajectoryPoint.x = (startingPosition.x + n * stepVelocity.x + 0.5f * (n * n + n) * stepGravity.x);
trajectoryPoint.y = (startingPosition.y + n * stepVelocity.y + 0.5f * (n * n + n) * stepGravity.y);
return trajectoryPoint;
}
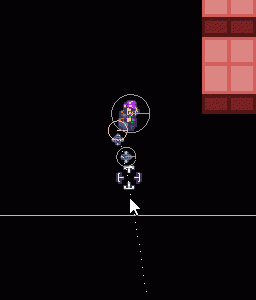
Графические результаты (Как вы можете видеть, я не получаю желаемых результатов..)
Возможно решение (я нашел это решение , вычисляя начальные скорости при заданной траектории параболы , но мне трудно преобразовать это в box2d.)
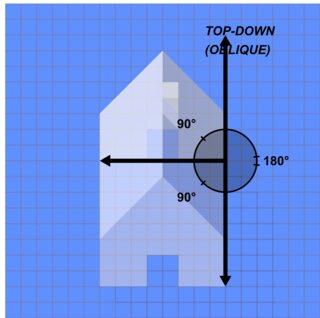
Обновление (8/6/2016) дополнительные сведения для ссылки на проекцию
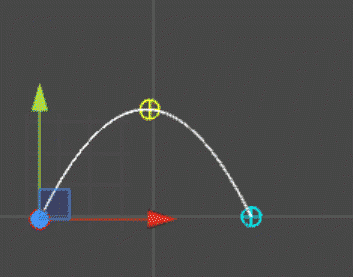
На приведенном ниже изображении представлена графическая проекция сверху вниз (косая).
1 ответ:
Этот ответ использует понятия, распространенные в разработке игр, поэтому может быть целесообразно перенести этот вопрос в GameDev.StackExchange .
1. Системы координат
Поскольку вы пытаетесь имитировать трехмерное движение на 2D-дисплее, полезным начальным шагом является разделение ваших концепций мирового пространства и экранного пространства
Мировое пространство - это виртуальная система координат, в которой расположен мир вашей игры. в которой моделируется его механика. Чтобы смоделировать дугообразное движение снаряда, который имеет высоту от плоскости 2D земли, вы хотите использовать трехмерную систему координат (x, y, z).
Чтобы свести к минимуму конфликты с вашей текущей схемой, предположим, что z-это направление, указывающее "вверх" от плоскости пола (x,y), которую вы используете в данный момент. Если вам не нужно моделировать объекты, проходящие над / под друг другом, то вы можете продолжать имитировать свою физику в 2D только с компонентами (x,y), неявно обрабатывая координата z равна 0.Экранное пространство - это система координат, которую вы фактически используете для визуализации. Чтобы взять трехмерную координату мирового пространства и преобразовать ее в двумерную плоскость экрана, вам потребуется применить проекцию . Для игры, подобной той, которую вы показали, вы можете использовать наклонную проекцию сверху вниз, что-то вроде....
Это будет представлять ваш мир без ракурса (так что круг на полу становится кругом на полу). ваш экран, и прыжок на 1 м вверх смещает персонажа так же, как ходьба на 1 м "Север").
screenPos.x = (worldPos.x - cameraOffset.x) * zoomFactor; screenPos.y = (worldPos.y + worldPos.z - cameraOffset.y) * zoomFactor;Если вы хотите более реалистичный взгляд, вы можете умножить worldPos.y & worldPos.z на некоторые коэффициенты меньше 1,0 для моделирования ракурса (таким образом, круг на полу становится эллипсом на экране)
2. Моделирование задачи в двух частях
Имея в виду это различие, мы можем рассматривать снаряд в вашем примере как два отдельных снаряда. части:
Тень движется вдоль двумерной плоскости пола, (x, y, 0). Поскольку ваша физика 2D, имеет смысл рассматривать тень как "реальный" снаряд, управляемый вашей физикой Box2D, и основывать свои столкновения на ее движении.
Т. е. Когда тень снаряда пересекает след цели, снаряд попадает в цель.
(Если вы хотите более высокую точность, так что снаряд может быть брошен поверх короткого объекта, чтобы приземляйтесь на пол с другой стороны, вам нужно будет либо перейти к 3D-физическому моделированию, либо использовать некоторые проверки высоты, чтобы выборочно игнорировать столкновения)
Баллистическая пуля - это часть, которая проходит по дуге в воздухе. Мы можем думать об этом как о чисто визуальном эффекте, без связанных с ним физических столкновений. (Чтобы понять, почему, посмотрите на пример gif, когда персонаж стреляет вниз: пуля сначала летит вверх позади него - но мы не хотели бы, чтобы пуля попала во врага позади игрока, когда они пытаются стрелять вниз перед своим персонажем)
3. Тень
Это ведет себя примерно так же, как вы, вероятно, уже обращаетесь с прямыми пулями в своей игре. Просто направьте его в направлении от вашего дула к вашей цели и установите его скорость. Основная 2D физика без гравитации возьмет его оттуда.float bulletSpeed = 6; Vector2 touchPoint = ScreenToWorldPoint(input.touchpoint.x, input.touchpoint.y); Vector2 targetOffset = touchPoint.cpy().sub(firingPosition); Vector2 targetDirection = targetOffset.cpy().nor(); Vector2 targetVelocity = targetDirection.cpy().scl(bulletSpeed); shadowBody.setLinearVelocity(targetVelocity);Поскольку игровая механика здесь 2D, я бы рекомендовал держать скорость стрельбы постоянной, как у вас это выше. Это сделает поведение оружия более последовательным и предсказуемым для игрока. Чтобы стрелять из настоящего оружия дальше, мы часто направляли его вверх, жертвуя некоторой горизонтальной скоростью для вертикальной, чтобы противостоять гравитации, так как наша цель удаляется, наше время до попадания растет нелинейно. В случае этой игры, хотя баллистическая дуга на самом деле просто искусственный визуальный эффект, так что спорно, действительно ли добавление этого физического реализма делает его лучше. Я бы попробовал без него и увидел скучаете ли вы по нему. ;)
4. Дуга баллистической пули
Есть несколько вариантов того, как мы стилизуем дугу. Мы могли бы попытаться всегда достигать определенной высоты или поддерживать определенную скорость запуска и т. д. Для дальнейшего Я собираюсь предложить использовать постоянную величину гравитации и выбрать начальную скорость движения вверх, достаточную для приземления, когда тень достигаетinput.touchPoint. Это будет иметь тенденцию давать более мелкие дуги / более прямые выстрелы по ближайшим целям и более высокие поля, когда стрельба вдалеке.Во-первых, некоторые настраиваемые константы:
// Tune this to get the arcs the height/sharpness you want. float gravity = 9.8f; // Tune this until it matches the height of your character's muzzle off the ground. float launchHeight = 1.0f;Далее мы запускаем пулю в соответствующую точку над местом на полу, откуда она должна быть выпущена:
Теперь, основываясь на значениях, которые мы рассчитали выше для перемещения тени, мы можем вычислить начальную восходящую скорость пули:bullet.worldPos.x = firingPosition.x; bullet.worldPos.y = firingPosition.y; bullet.worldPos.z = launchHeight;float distance = targetDirection.dot(targetOffset); // 2D range to target float duration = distance/bulletSpeed; // Time until hit // Initialize its vertical (z) velocity to create the arc we want. // See section 5 below for how this formula is derived. bullet.verticalVelocity = duration * gravity/2 - launchHeight/duration;Теперь каждый кадр (после каждого шага физики) мы можем сделать следующее, Чтобы обновить пулю до соответствующего положения над ее тень:
Здесь я использую интегрирование Эйлера для моделирования дуги, которое является простым, но может показать ошибки аппроксимации, если у вас низкая/неравномерная частота кадров. Вероятно, это не очень важно для такого визуального эффекта, но если вы хотите более высокой точности, вы можете отслеживать время огня или время в воздухе и использовать параметрическое уравнение дляbullet.worldPos.x = shadow.worldPos.x; bullet.worldPos.y = shadow.worldPos.y; bullet.verticalVelocity -= gravity * deltaTime; bullet.worldPos.z += bullet.verticalVelocity * deltaTime; // Convert to screen space using a projection like the oblique style described above. bullet.screenPos = Project(bullet.worldPos);h(t)ниже, чтобы точно проследить дугу. [19]}5. Вывод (опционально)Если вам интересно, как мы рассчитываем начальную скорость выше:
Мы знаем, что нам нужна парабола, которая достигает нуля в момент времени t = длительность, с кривизной из-за гравитации. Это дает нам квадратичную форму со следующей факторизованной формой....h(t) = -g/2 * (t - duration) * (t - p)...по какой-то неизвестной п...
h(t) = (-g/2) * p * duration + (g/2)*(duration + p) * t - (g/2) * t*tУстановка t = 0 дает нам начальную высоту запуска, которую мы можем решить для
pПодставляя в развернутую форму h(t) выше, получим...h(0) = (-g/2) * p * duration p = -2 * h(0) / (g * duration)h(t) = h(0) + ((g/2)*duration - h(0)/duration) * t - (g/2) * t*tИ этот средний член, линейный в
t, является начальным вертикальная скорость. (Первый член-это начальная высота, а последний член-ускорение, вызванное гравитацией)