Как оценить оставшееся время загрузки (точно)?
Конечно, вы можете разделить оставшийся размер файла на текущую скорость загрузки, но если ваша скорость загрузки колеблется (а она будет), это не дает очень хорошего результата. Каков лучший алгоритм для получения более плавного обратного отсчета?
5 ответов:
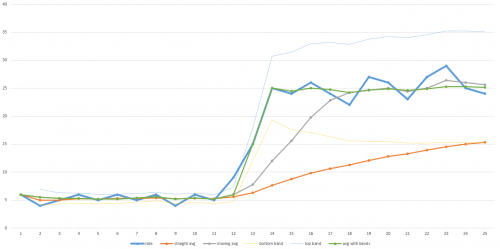
Много лет назад я написал алгоритм для прогнозирования времени, оставшегося в программе формирования образа диска и многоадресной рассылки, которая использовала скользящую среднюю со сбросом, когда текущая пропускная способность выходила за пределы заданного диапазона. Он сохранял бы все гладко, если бы не произошло что-то радикальное, затем он быстро адаптировался бы и снова вернулся к скользящей средней. Смотрите пример диаграммы здесь:
Толстая синяя линия в этом примере диаграммы является фактической пропускной способностью с течением времени. Уведомление низкая пропускная способность в течение первой половины передачи, а затем она резко подскакивает во второй половине. Оранжевая линия - это общее среднее значение. Обратите внимание, что он никогда не настраивается достаточно далеко, чтобы когда-либо дать точный прогноз того, сколько времени потребуется, чтобы закончить. Серая линия-это скользящая средняя (то есть среднее значение последних N точек данных - на этом графике N равно 5, но в действительности N может быть больше, чтобы сгладить достаточно). Он восстанавливается быстрее, но все равно требуется время, чтобы приспособиться. Оно займет больше времени, чем крупнее Н. Так что если ваши данные довольно шумные, то N должно быть больше, и время восстановления будет больше.
Зеленая линия-это алгоритм, который я использовал. Он движется точно так же, как скользящая средняя, но когда данные выходят за пределы заданного диапазона (обозначенного тонкими синими и желтыми линиями), он сбрасывает скользящую среднюю и сразу же прыгает вверх. Предварительно определенный диапазон также может быть основан на стандартном отклонении, поэтому он может подстраиваться под уровень шума данных. автоматически. Я просто бросил эти значения в Excel, чтобы построить диаграмму для этого ответа, поэтому он не идеален, но вы понимаете идею.
Данные можно было бы придумать, чтобы этот алгоритм не был хорошим предсказателем оставшегося времени. Суть в том, что вам нужно иметь общее представление о том, как вы ожидаете, что данные будут вести себя, и выбрать алгоритм соответственно. Мой алгоритм хорошо работал для наборов данных, которые я видел, поэтому мы продолжали использовать его.
Еще один важный совет заключается в том, что обычно разработчики игнорируют время установки и демонтажа в своих индикаторах прогресса и расчетах оценки времени. Это приводит к Вечному 99% или 100% прогресс-бару, который просто сидит там в течение длительного времени (в то время как кэш очищается или происходит другая работа по очистке) или диким ранним оценкам, когда происходит сканирование каталогов или другая работа по настройке, накапливается время, но не накапливается какой-либо процент прогресса, который отбрасывает все. Вы можете выполнить несколько тестов, которые включают время установки и демонтажа и придумайте оценку того, как долго это время в среднем или на основе размера задания, и добавьте это время в индикатор выполнения. Например, первые 5% работы-это работа по настройке,а последние 10% - работа по демонтажу, а затем 85% в середине-это загрузка или любой другой повторяющийся процесс отслеживания. Это тоже может очень помочь.
Экспоненциальная скользящая средняя отлично подходит для этого. Это позволяет сгладить среднее значение, так что каждый раз, когда вы добавляете новую выборку, старые выборки становятся все менее важными для общего среднего. Они все еще рассматриваются, но их важность падает экспоненциально-отсюда и название. А так как это" скользящее " среднее, вам нужно только держать одно число вокруг.
В контексте измерения скорости загрузки формула будет выглядеть так: это:
averageSpeed = SMOOTHING_FACTOR * lastSpeed + (1-SMOOTHING_FACTOR) * averageSpeed;
SMOOTHING_FACTORэто число между 0 и 1. Чем выше это число, тем быстрее отбрасываются старые образцы. Как вы можете видеть в Формуле, когдаSMOOTHING_FACTORравно 1, вы просто используете значение вашего последнего наблюдения. КогдаSMOOTHING_FACTORравно 0averageSpeedникогда не меняется. Итак, вы хотите что-то среднее, и обычно низкое значение, чтобы получить приличное сглаживание. Я обнаружил, что 0.005 обеспечивает довольно хорошее значение сглаживания для средней скорости загрузки.
lastSpeedэто последняя измеренная скорость загрузки. Вы можете получить это значение, запустив таймер каждую секунду или около того, чтобы вычислить, сколько байт было загружено с момента последнего запуска.
averageSpeedэто, очевидно, число, которое вы хотите использовать для расчета вашего расчетного оставшегося времени. Инициализируйте это до первого измеренияlastSpeed, которое вы получите.
Я думаю, что лучшее, что вы можете сделать, это разделить оставшийся размер файла на среднюю скорость загрузки (загруженный до сих пор разделен с тем, как долго вы загружали). Это будет колебаться немного, чтобы начать, но будет все более и более стабильным, чем дольше вы загружаете.
В дополнение к ответу Бена Долмана вы также можете вычислить флуктуацию в рамках алгоритма. Он будет более плавным, но он также будет предсказывать среднюю скорость.
Что-то вроде этого:
Флуктуация или нет, он будет таким же стабильным, как и другой, с правильными значениями для прогнозирования и depencySpeed; вам придется немного поиграть с ним в зависимости от скорости вашего интернета. Эти настройки идеально подходят для средней скорости 600 кб/с, когда она колеблется от 0 до 1 МБ.prediction = 50; depencySpeed = 200; stableFactor = .5; smoothFactor = median(0, abs(lastSpeed - averageSpeed), depencySpeed); smoothFactor /= (depencySpeed - prediction * (smoothFactor / depencySpeed)); smoothFactor = smoothFactor * (1 - stableFactor) + stableFactor; averageSpeed = smoothFactor * lastSpeed + (1 - smoothFactor) * averageSpeed;