Извлеките случайные числа из смеси однородных распределений

Цель

Я пытаюсь построить функцию, которая извлекает определенное число случайных чисел из "неполного равномерного распределения".

Что я называю неполным равномерным распределением?

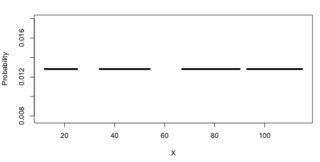
Неполное равномерное распределение я называю распределением вероятностей, где каждое значение X в пределах ряда границ имеет равную вероятность быть выбранным. Другими словами, это равномерное распределение с отверстиями (где вероятность равна нулю), как представленный ниже 
x = list(12:25, 34:54, 67:90, 93:115)
y = 1/sum(25-12, 54-34, 90-67, 115-93)
plot(y=rep(y, length(unlist(x))), x=unlist(x), type="n", ylab="Probability", xlab="X")
for (xi in x)
{
    points(xi,rep(y, length(xi)), type="l", lwd=4)
}

Введите описание изображения здесь

Уродливое Решение

Вот медленное и уродливое решение 

IncompleteUnif = function(n,b)
{
    #################
    # "n" is the desired number of random numbers
    # "b" is a list describing the boundaries within which a random number can possibly be drawn.
    #################
    r = c() # Series of random numbers to return
    for (ni in n)
    {
        while (length(r) < n) # loop will continue until we have the "n" random numbers we need
        {
            ub = unlist(b)
            x = runif(1,min(ub), max(ub)) # one random number taken over the whole range
            for (bi in b) # The following loop test if the random number is withinn the ranges specified by "b"
            {
                if (min(bi) < x & max(bi) > x) # if found in one range then just add "x" to "r" and break
                {
                    r = append(r,x)
                    break
                }
            }
        }
    }
    return (r)
}

b = list(c(5,94),c(100,198),c(220,292), c(300,350))
set.seed(12)
IncompleteUnif(10,b)
[1]  28.929516 287.132444 330.204498  63.425103  16.693990  66.680826 226.374551  12.892821   7.872065 140.480533
5 3
random distribution

5 ответов:

Слегка запутанная версия решения @Gregor.

mix_unif <- function(n, b){
  x <- c()
  ns <- rmultinom(1, n, sapply(b, diff))
  for (i in seq_along(ns)) {
    x <- c(x, runif(ns[i], b[[i]][1], b[[i]][2]))
  }
  x
}

microbenchmark(mix_unif(1e5, b),
               rmixunif(1e5, b),
               IncompleteUnif(1e5, b), 
               unit="relative")
Unit: relative
                     expr      min       lq     mean   median       uq      max neval
       mix_unif(1e+05, b) 1.000000 1.000000 1.000000 1.000000 1.000000  1.00000   100
       rmixunif(1e+05, b) 3.123515 3.235961 3.750369 3.496843 3.462529 15.73449   100
 IncompleteUnif(1e+05, b) 6.806916 7.247425 6.926282 7.188556 7.093928 18.20041   100
4

Ваше неполное равномерное распределение можно представить как смесь четырех обычных равномерных распределений, причем вес смешивания для каждого сегмента пропорционален его длине (т. е. Так, что чем длиннее сегмент, тем больший вес он имеет).

Для выборки из такого распределения сначала выберите сегмент (с учетом весов). Затем из выбранного сегмента выберите элемент.

5

Я считаю, что это работает, используя алгоритм, предложенный Робертом Додье:

rmixunif = function(n, b) {
    subdists = sample(seq_along(b), size = n, replace = T, prob = sapply(b, diff))
    subdists_n = tabulate(subdists)
    draw = numeric(n)
    for (i in unique(subdists)) {
        draw[subdists == i] = runif(subdists_n[i], min = b[[i]][1], max = b[[i]][2])
    }
    return(draw)
}

rmixunif(10, b = list(c(5,94),c(100,198),c(220,292), c(300,350)))
#  [1]  64.85989  85.33292 235.39607 233.40133 240.28686  67.21626 237.60248  11.80377 151.65365 306.44473

Мне нравится визуальная проверка гистограммы Сэма Диксона, вот моя версия: 

x <- rmixunif(10000,list(c(0,1),c(2.5,3),c(6,10)))
hist(x,breaks=20)

Введите описание изображения здесь

Это может быть придумано с некоторой проверкой ввода (и, возможно, mapply , как предложено в комментариях), но я оставлю это другим.

Спасибо alexis_iaz за предложение tabulate()!

4

Другим решением является преобразование выходных данных. Идея состоит в том, чтобы взять выборку из случайного равномерного распределения, а затем применить условное преобразование так, чтобы числа попадали только в выбранные диапазоны: 

IncompleteUnif = function(n,b) {
  widths <- cumsum(sapply(b,diff))
  x <- runif(n,0,tail(widths,1))
  out <- x
  out[x<=widths[1]] <- x[x<=widths[1]] + b[[1]][1]
  for(i in 2:length(b)) {
    out[widths[i-1]<x & x<=widths[i]] <- x[widths[i-1]<x & x<=widths[i]] - widths[i-1] + b[[i]][1]
  }
  return(out)
}

x <- IncompleteUnif(10000,list(c(0,1),c(2.5,3),c(6,10)))
hist(x,breaks=20)

Введите описание изображения здесь

2

Я на несколько лет опоздал на вечеринку, но, видя, что еще не было решения без явного цикла, вот одна такая реализация (следуя подходу @RobertDodier): 

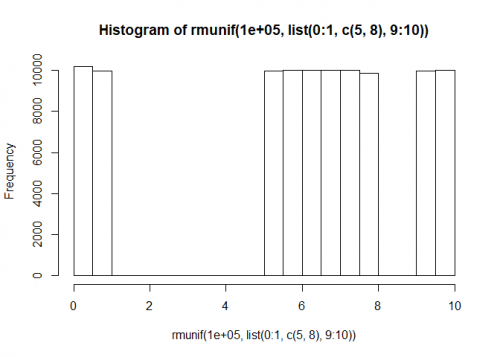
rmunif <- function(n, b) {
  runifb <- function(n, b) runif(n, b[1], b[2])
  ns <- rmultinom(1, n, vapply(b, diff, 1))
  unlist(Map(runifb, ns, b), use.names = FALSE)
}

hist(rmunif(1e5, list(0:1, c(5, 8), 9:10)))


library(microbenchmark)

set.seed(2018)
n <- 1e5

microbenchmark(
  rmunif(n, b),
  mix_unif(n, b),
  rmixunif(n, b),
  IncompleteUnif(n, b),
  unit = "relative"
) -> mb

print(mb, signif = 5)
#> Unit: relative
#>                  expr    min     lq   mean median     uq    max neval
#>          rmunif(n, b) 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000   100
#>        mix_unif(n, b) 1.1181 1.1256 1.1281 1.1728 1.1236 1.0476   100
#>        rmixunif(n, b) 2.7822 2.8982 2.9899 2.7850 2.8345 1.3970   100
#>  IncompleteUnif(n, b) 4.4922 4.7089 5.2732 4.5764 8.4317 2.4364   100

Создан на 2018-03-11 с помощью пакета reprex (v0.2.0).

0