Используя lm (), nls () (и glm ()?) оценить темпы роста населения в мальтузианской модели роста
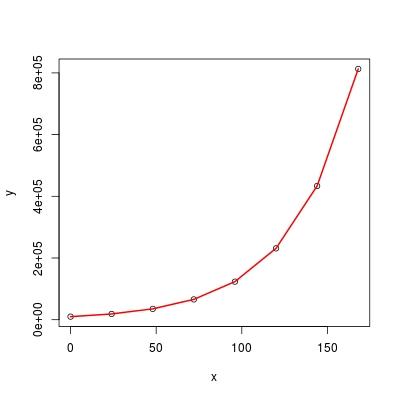
Мой вопрос имеет отношение к оценке темпов роста численности населения в модель роста Мальтуса. В качестве примера игрушки рассмотрим набор данных игрушек df:
structure(list(x= c(0L, 24L, 48L, 72L, 96L, 120L, 144L, 168L
), y = c(10000, 18744.0760659189, 35134.0387564953, 65855.509495469,
123440.067934292, 231377.002294256, 433694.813090781, 812920.856596808
)), .Names = c("x", "y"), row.names = c(NA, -8L), class = "data.frame")
Я пытаюсь соответствовать этому набору данных с помощью экспоненциальной модели :
y = 10000 * (e^(r * x))
И оценка r. При использовании нелинейной регрессии nls():
fit <- nls(y ~ (10000 * exp(r*x)), data=df)
Я получаю следующую ошибку:
Error in getInitial.default(func, data, mCall = as.list(match.call(func, :
no 'getInitial' method found for "function" objects
Я тоже пытался lm()
fit <- lm(log(y) ~ (10000 * exp(r*x)), data=df)
Но получить
Error in terms.formula(formula, data = data) :
invalid model formula in ExtractVars
Как я могу это решить? Как могу ли я подогнать данные к экспоненциальной модели, которая у меня есть?
Кроме того, существуют ли другие подходы, которые я мог бы рассмотреть для подгонки модели роста населения? Является ли glm() разумным?
1 ответ:
Использование lm()
Пожалуйста, прочитайте
?formulaдля правильной спецификации формулы. Теперь я продолжу, предполагая, что вы это прочитали.Во-первых, ваша модель, приняв преобразование
logкак на LHS, так и на RHS, становится:Константа-это известное значение, не подлежащее оценке. Такая константа называетсяlog(y) = log(10000) + r * xoffsetвlm.Вы должны использовать
lmследующим образом:# "-1" in the formula will drop intercept fit <- lm(log(y) ~ x - 1, data = df, offset = rep(log(10000), nrow(df))) # Call: # lm(formula = log(y) ~ x - 1, data = df, offset = rep(log(10000), nrow(df))) # Coefficients: # x # 0.02618Как вы заметили,
fit- это список длиной 13. См. раздел "значение" в разделе И вы получите лучшее представление о том, что они собой представляют. Среди них подходящие значения$fitted, так что вы можете нарисовать свой участок по:Обратите внимание на то, что я используюplot(df) lines(df$x, exp(fit$fitted), col = 2, lwd = 2) ## red lineexp(fit$fitted), потому что мы подходим к модели дляlog(y), и теперь мы возвращаемся к первоначальному масштабу.Замечание
Как сказал @BenBolker, более простая спецификация:fit <- lm(log(y/10000) ~ x - 1, data = df)Или
fit <- lm(log(y) - log(10000) ~ x - 1, data = df)Но переменная ответа не
log(y), аlog(y/10000)сейчас, так что когда вы сделайте заговор, вам нужно:lines(df$x, 10000 * exp(fit$fitted), col = 2, lwd = 2)
Использование
nls()Правильный способ использования
nls()таков:Поскольку нелинейная подгонка кривой требует итераций, необходимо начальное значение, и должно быть предоставлено через аргументnls(y ~ 10000 * exp(r * x), data = df, start = list(r = 0.1))start.Теперь, если вы попробуете этот код, вы получите:
Error in nls(y ~ 10000 * exp(r * x), data = df, start = list(r = 0.1)) : number of iterations exceeded maximum of 50Проблема заключается в том, что ваши данные точны, без шума. Прочтите на
?nls:Warning: *Do not use ‘nls’ on artificial "zero-residual" data.*Итак, используя
nls()для набора данных вашей игрушкиdfне работает.Давайте вернемся к проверке установленной модели из
lm():fit$residuals # 1 2 3 4 5 #-2.793991e-16 -1.145239e-16 -2.005405e-15 -5.498411e-16 3.094618e-15 # 6 7 8 # 1.410007e-15 -1.099682e-15 -1.007937e-15Остатки в основном равны 0 везде, и
lm()в этом случае точно соответствует.
Последующие действия
Еще одна вещь, которую я не смог выяснить, - это почему параметр
rне используется в спецификации формулыlm.На самом деле есть некоторая разница в Формуле между
lmиnls. Возможно, ты сможешь. примите это как таковое:
- Формула
lm()называется формулой модели, которую можно прочитать из?formula. Она настолько фундаментальна в R. процедуры подгонки модели используют ее, какlm,glm, в то время как многие функции имеют метод формулы, какmodel.matrix,aggregate,boxplot, и т.д.- Формула
nls()больше похожа на спецификацию функции и действительно не широко используется. Многие другие функции, выполняющие нелинейные итерации, такие какoptim, не принимают формулу, но принимают функцию непосредственно. Так что, просто рассматривайтеnls()как частный случай.Так есть ли смысл делать это с помощью линейной модели? Просто то, что я пытаюсь смоделировать здесь, - это использование мальтузианской модели роста.Строго говоря, предоставление реальных данных о населении (конечно, с шумом), использованиеnls()для подгонки кривой или использованиеglm(, family = poisson)для реакции Пуассона GLM имеет лучшую основу, чем подгонка линейной модели. Вызовglm()для ваших данных будет следующим:glm(y ~ x - 1, family = poisson(), data = df, offset = rep(log(10000), nrow(df)))(возможно, вам нужно узнать, что ГЛМ-это первое.) Но так как ваши данные не имеют шума, вы получите предупреждающее сообщение при его использовании.
Однако с точки зрения вычислительной сложности использование линейной модели путем первого преобразованияlogявляется очевидным выигрышем. В статистическом моделировании переменные преобразования очень распространены, поэтому нет никаких веских причин отказываться от использования линейной модели для оценки темпов роста населения.В качестве полной картины я рекомендую вам попробовать все три подхода по-настоящему данные (или шумные игрушечные данные). Будет некоторая разница в оценках и прогнозах, но вряд ли она будет очень большой.
"Follow-follow-up"
Ха-ха, еще раз спасибо @Ben. Для
glm()Мы также можем попробовать:glm(y ~ x - 1 + offset(log(10000)), family = gaussian(link="log"))Для спецификации
offsetмы можем либо использовать аргументoffsetвlm/glm, или функциюoffset(), как это делает Бен.