Интерпретация реальных / воображаемых / АБС частей БПФ

В настоящее время я изучаю дискретное преобразование Фурье и играю с numpy, чтобы лучше понять его.

Я попытался построить сигнал "sin x sin x sin" и получил чистый FFT с 4 ненулевыми точками. Я наивно сказал себе : "ну, если я построю сигнал" sin + sin + sin + sin "с этими амплитудами и частотами, я должен получить тот же сигнал "sin x sin x sin", верно?

Хорошо... не совсем

(Первый-сигнал" x", второй -" +" Сигнал)

Введите описание изображения здесь

Оба имеют одинаковые амплитуды / частоты, но не являются одинаковыми сигналами, даже если я вижу, что они имеют некоторое сходство.

Хорошо, так как я построил только абсолютные значения FFT, я думаю, что потерял некоторую информацию.

Затем я построил действительную часть, мнимую часть и абсолютные значения для обоих сигналов: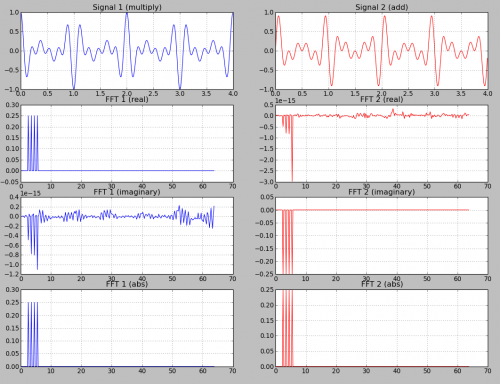

Введите описание изображения здесь

Теперь я в замешательстве. Что мне со всем этим делать? Я читал о ДФТ с математической точки зрения. Я понимаю этот комплекс. значения приходят из единичного круга. Мне даже пришлось узнать о гильбертовом пространстве, чтобы понять, как оно работает (и это было больно!...а я только поцарапал поверхность). Я только хочу понять, имеют ли эти реальные / воображаемые сюжеты какой-либо конкретныйсмысл вне математического мира:
  • abs (fft) : частоты + амплитуды
  • real (fft):?
  • воображаемое (fft):?

Код: 

import numpy as np
import matplotlib.pyplot as plt
N = 512 # Sample count
fs = 128 # Sampling rate
st = 1.0 / fs # Sample time
t = np.arange(N) * st # Time vector

signal1 = 
1   *np.cos(2*np.pi * t) *
2   *np.cos(2*np.pi * 4*t) *
0.5 *np.cos(2*np.pi * 0.5*t)

signal2 = 
0.25*np.sin(2*np.pi * 2.5*t) +
0.25*np.sin(2*np.pi * 3.5*t) +
0.25*np.sin(2*np.pi * 4.5*t) +
0.25*np.sin(2*np.pi * 5.5*t)



_, axes = plt.subplots(4, 2)

# Plot signal
axes[0][0].set_title("Signal 1 (multiply)")
axes[0][0].grid()
axes[0][0].plot(t, signal1, 'b-')

axes[0][1].set_title("Signal 2 (add)")
axes[0][1].grid()
axes[0][1].plot(t, signal2, 'r-')

# FFT + bins + normalization
bins = np.fft.fftfreq(N, st)    
fft  = [i / (N/2) for i in np.fft.fft(signal1)]
fft2 = [i / (N/2) for i in np.fft.fft(signal2)]

# Plot real
axes[1][0].set_title("FFT 1 (real)")
axes[1][0].grid()
axes[1][0].plot(bins[:N/2], np.real(fft[:N/2]), 'b-')

axes[1][1].set_title("FFT 2 (real)")
axes[1][1].grid()
axes[1][1].plot(bins[:N/2], np.real(fft2[:N/2]), 'r-')

# Plot imaginary
axes[2][0].set_title("FFT 1 (imaginary)")
axes[2][0].grid()
axes[2][0].plot(bins[:N/2], np.imag(fft[:N/2]), 'b-')

axes[2][1].set_title("FFT 2 (imaginary)")
axes[2][1].grid()
axes[2][1].plot(bins[:N/2], np.imag(fft2[:N/2]), 'r-')

# Plot abs
axes[3][0].set_title("FFT 1 (abs)")
axes[3][0].grid()
axes[3][0].plot(bins[:N/2], np.abs(fft[:N/2]), 'b-')

axes[3][1].set_title("FFT 2 (abs)")
axes[3][1].grid()
axes[3][1].plot(bins[:N/2], np.abs(fft2[:N/2]), 'r-')

plt.show()
3 8
numpy signal-processing fft complex-numbers

3 ответа:

Для каждого частотного Бина величина sqrt(re^2 + im^2) сообщает вам амплитуду компонента на соответствующей частоте. Фаза atan2(im, re) сообщает вам относительную фазу этого компонента. Реальные и воображаемые части сами по себе не особенно полезны.

16

Относительно некоторой опорной точки, скажем, центра фиксированного временного окна, синусоида и косинусоида одной и той же частоты будут выглядеть по-разному (иметь разные начальные фазы относительно любой фиксированной временной опорной точки). Они также будут математически ортогональны по любой целочисленной периодической ширине, поэтому могут представлять независимые компоненты базисного вектора преобразования.

Реальная часть результата БПФ - это то, насколько каждая частотная составляющая похожа на косинусную волну, воображаемая составляющая, насколько каждая составляющая напоминает синусоиду. Различные соотношения синусоидальных и косинусоидальных составляющих вместе позволяют построить синусоиду любой произвольной или желаемой фазы, что позволяет получить полный результат БПФ.

Одна только величина не может определить разницу между синусоидной и косинусной волнами. IFFT(imag (FFT)) испортил бы реконструкцию любого сигнала с другой фазой, чем чистые косинусы. То же самое с IFFT (re (FFT)) и чистыми синусоидальными волнами (относительно Окно диафрагмы БПФ).
4

Сигнал 1, состоящий из произведения трех функций cos, можно преобразовать в сумму четырех функций cos. Это имеет значение для функции 2, которая является суммой четырех синусоидальных функций.

Функция cos является четной функцией cos (- x) == cos (x). Преобразование Фурье четной функции является чисто реальным. Именно поэтому график мнимой части БПФ функции 1 содержит только значения, близкие к нулю (1е-15).

Функция синуса является нечетной функцией sin (- x) = = - sin (x). Преобразование Фурье нечетной функции является чисто мнимым. Именно поэтому график действительной части БПФ функции 2 содержит только значения, близкие к нулю (1е-15).

Если вы хотите понять БПФ и ДПФ более подробно, прочитайте учебник анализа сигналов для электротехники.

1