Интеграция многомерных неотъемлемой составляющей
Мотивация: у меня есть многомерный Интеграл, который для полноты картины я воспроизвел ниже. Он исходит из вычисления второго вириального коэффициента при наличии значительной анизотропии:
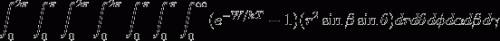
Здесь W-функция всех переменных. Это известная функция, для которой я могу определить функцию python.
Вопрос программирования: Как мне получить scipy, чтобы интегрировать это выражение? Я думал о цепочке из двух тройных квадроциклов (scipy.integrate.tplquad) вместе, но я беспокоюсь о производительности и точности. Существует ли в scipy интегратор более высокой размерности, который может обрабатывать произвольное число вложенных интегралов? Если нет, то как лучше всего это сделать?
3 ответа:
С таким многомерным интегралом, как этот, методы Монте-Карло часто полезны - они сходятся к ответу в виде обратного квадратного корня из числа оценок функций, что лучше для более высокой размерности, тогда вы вообще выйдете из даже довольно сложных адаптивных методов (если вы не знаете что - то очень специфическое о ваших подынтегральных симметриях, которые можно использовать и т. д.)
Пакетmcint выполняет интегрирование по методу Монте-Карло: выполняется с нетривиальной
W, которая тем не менее интегрируема, поэтому мы знаем ответ, который мы получаем (обратите внимание, что я усек r, чтобы быть из [0,1); вам придется сделать какое-то логарифмическое преобразование или что-то, чтобы получить эту полубесконечную область в нечто, поддающееся обработке для большинства числовых интеграторов):import mcint import random import math def w(r, theta, phi, alpha, beta, gamma): return(-math.log(theta * beta)) def integrand(x): r = x[0] theta = x[1] alpha = x[2] beta = x[3] gamma = x[4] phi = x[5] k = 1. T = 1. ww = w(r, theta, phi, alpha, beta, gamma) return (math.exp(-ww/(k*T)) - 1.)*r*r*math.sin(beta)*math.sin(theta) def sampler(): while True: r = random.uniform(0.,1.) theta = random.uniform(0.,2.*math.pi) alpha = random.uniform(0.,2.*math.pi) beta = random.uniform(0.,2.*math.pi) gamma = random.uniform(0.,2.*math.pi) phi = random.uniform(0.,math.pi) yield (r, theta, alpha, beta, gamma, phi) domainsize = math.pow(2*math.pi,4)*math.pi*1 expected = 16*math.pow(math.pi,5)/3. for nmc in [1000, 10000, 100000, 1000000, 10000000, 100000000]: random.seed(1) result, error = mcint.integrate(integrand, sampler(), measure=domainsize, n=nmc) diff = abs(result - expected) print "Using n = ", nmc print "Result = ", result, "estimated error = ", error print "Known result = ", expected, " error = ", diff, " = ", 100.*diff/expected, "%" print " "Бег дает
Using n = 1000 Result = 1654.19633236 estimated error = 399.360391622 Known result = 1632.10498552 error = 22.0913468345 = 1.35354937522 % Using n = 10000 Result = 1634.88583778 estimated error = 128.824988953 Known result = 1632.10498552 error = 2.78085225405 = 0.170384397984 % Using n = 100000 Result = 1646.72936 estimated error = 41.3384733174 Known result = 1632.10498552 error = 14.6243744747 = 0.8960437352 % Using n = 1000000 Result = 1640.67189792 estimated error = 13.0282663003 Known result = 1632.10498552 error = 8.56691239895 = 0.524899591322 % Using n = 10000000 Result = 1635.52135088 estimated error = 4.12131562436 Known result = 1632.10498552 error = 3.41636536248 = 0.209322647304 % Using n = 100000000 Result = 1631.5982799 estimated error = 1.30214644297 Known result = 1632.10498552 error = 0.506705620147 = 0.0310461413109 %Вы можете значительно ускорить это, векторизируя генерацию случайных чисел и т. д.
Конечно, вы можете связать тройные интегралы, как вы предлагаю:
Это медленно, но дает очень хорошие результаты для этого простого случая. Что лучше, будет зависеть от того, насколько сложен вашimport numpy import scipy.integrate import math def w(r, theta, phi, alpha, beta, gamma): return(-math.log(theta * beta)) def integrand(phi, alpha, gamma, r, theta, beta): ww = w(r, theta, phi, alpha, beta, gamma) k = 1. T = 1. return (math.exp(-ww/(k*T)) - 1.)*r*r*math.sin(beta)*math.sin(theta) # limits of integration def zero(x, y=0): return 0. def one(x, y=0): return 1. def pi(x, y=0): return math.pi def twopi(x, y=0): return 2.*math.pi # integrate over phi [0, Pi), alpha [0, 2 Pi), gamma [0, 2 Pi) def secondIntegrals(r, theta, beta): res, err = scipy.integrate.tplquad(integrand, 0., 2.*math.pi, zero, twopi, zero, pi, args=(r, theta, beta)) return res # integrate over r [0, 1), beta [0, 2 Pi), theta [0, 2 Pi) def integral(): return scipy.integrate.tplquad(secondIntegrals, 0., 2.*math.pi, zero, twopi, zero, one) expected = 16*math.pow(math.pi,5)/3. result, err = integral() diff = abs(result - expected) print "Result = ", result, " estimated error = ", err print "Known result = ", expected, " error = ", diff, " = ", 100.*diff/expected, "%"Wи каковы ваши требования к точности. Простой (быстрый для оценки) W с высокой точностью подтолкнет вас к этому виду метода; сложный (медленный для оценки) W с умеренными требованиями к точности подтолкнет вас к методам MC.Result = 1632.10498552 estimated error = 3.59054059995e-11 Known result = 1632.10498552 error = 4.54747350886e-13 = 2.7862628625e-14 %
Я просто сделаю пару общих замечаний о том, как точно сделать этот вид интеграла, но этот совет не является специфическим для scipy (слишком длинный для комментария, даже если это не ответ).
Я не знаю вашего варианта использования, то есть удовлетворяетесь ли вы "хорошим" ответом с несколькими цифрами точности, которые можно было бы получить прямолинейно, используя Монте-Карло, как описано в ответе Джонатана Дурси, или вы действительно хотите продвинуть числовую точность до предела. возможный.
Я сам проводил аналитические, Монте-Карло и квадратурные вычисления вириальных коэффициентов. Если вы хотите сделать интегралы точно, то есть несколько вещей, которые вы должны сделать:
Попытайтесь выполнить как можно больше интегралов точно; вполне возможно, что интеграция в некоторых ваших координатах довольно проста.
Рассмотрите возможность преобразования переменных интегрирования таким образом, чтобы подынтегральное выражение было как можно более гладким. (Этот помогает как для Монте-Карло, так и для квадратуры).
Для Монте-Карло используйте выборку важности для наилучшей сходимости.
Для квадратуры с 7 интегралами можно просто получить очень быструю сходимость, используя квадратуру танх-Синха. Если вы можете получить его до 5 интегралов, то вы должны быть в состоянии получить 10-х цифр точности для вашего интеграла. Я настоятельно рекомендую mathtool / ARPREC для этой цели, доступный с домашней страницы Дэвида Бейли: http://www.davidhbailey.com/
Во-первых, чтобы сказать, что я не так хорош в математике, поэтому, пожалуйста, будьте добры. В любом случае, вот моя попытка:
Обратите внимание, что в вашем вопросе есть 6 переменные, но 7 интегралы!?
ВPythonиспользуяSympy:>>> r,theta,phi,alpha,beta,gamma,W,k,T = symbols('r theta phi alpha beta gamma W k T') >>> W = r+theta+phi+alpha+beta+gamma >>> Integral((exp(-W/(k*T))-1)*r**2*sin(beta)*sin(theta),(r,(0,2*pi)),(theta,(0,pi)),(phi,(0,2*pi)),(alpha,(0,2*pi)),(beta,(0,pi)),(gamma,(0,pi))) >>> integrate((exp(-W)-1)*r**2*sin(beta)*sin(theta),(r,(0,2*pi)),(theta,(0,pi)),(phi,(0,2*pi)),(alpha,(0,2*pi)),(beta,(0,pi)),(gamma,(0,pi)))И вот результат: [латексный код]
\begin{equation*}- \frac{128}{3} \pi^{6} - \frac{\pi^{2}}{e^{2 \pi}} - \frac{\pi}{e^{2 \pi}} - \frac{2}{e^{2 \pi}} - \frac{\pi^{2}}{e^{3 \pi}} - \frac{\pi}{e^{3 \pi}} - \frac{2}{e^{3 \pi}} - 3 \frac{\pi^{2}}{e^{6 \pi}} - 3 \frac{\pi}{e^{6 \pi}} - \frac{2}{e^{6 \pi}} - 3 \frac{\pi^{2}}{e^{7 \pi}} - 3 \frac{\pi}{e^{7 \pi}} - \frac{2}{e^{7 \pi}} + \frac{1}{2 e^{9 \pi}} + \frac{\pi}{e^{9 \pi}} + \frac{\pi^{2}}{e^{9 \pi}} + \frac{1}{2 e^{8 \pi}} + \frac{\pi}{e^{8 \pi}} + \frac{\pi^{2}}{e^{8 \pi}} + \frac{3}{e^{5 \pi}} + 3 \frac{\pi}{e^{5 \pi}} + 3 \frac{\pi^{2}}{e^{5 \pi}} + \frac{3}{e^{4 \pi}} + 3 \frac{\pi}{e^{4 \pi}} + 3 \frac{\pi^{2}}{e^{4 \pi}} + \frac{1}{2 e^{\pi}} + \frac{1}{2}\end{equation*}Вы можете сыграть немного больше для вашего вопроса;)