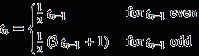int return_value = 1 / 2 * Terros(n - 1);
  int return_value = 1 / 2 * (3 * Terros(n - 1) + 1);

К сожалению, вы столкнулись с распространенной ошибкой, которую люди делают с ints.

(int)1 / (int) 2 всегда будет 0.

Так как 1/2 является целочисленным делением , то оно всегда 0; для того, чтобы исправить математику, просто поменять местами термины : не 1/2*n, а n/ 2; вместо 1/2* (3 * n + 1) поставить (3 * n + 1) / 2.

Еще один вопрос: не ставьте вычисление (Terros)и вывод (Console.WriteLine) в та же функция

public static String TerrosSequence(int n) {
  StringBuilder Sb = new StringBuilder();

  // Again: dynamic programming is far better here than recursion
  while (n > 1) {
    if (Sb.Length > 0)
      Sb.Append(",");

    Sb.Append(n);

    n = (n % 2 == 0) ? n / 2 : (3 * n + 1) / 2;
  }

  if (Sb.Length > 0)
    Sb.Append(",");

  Sb.Append(n);

  return Sb.ToString();
}


// Output: "Terros generated : 5,8,4,2,1"
Console.WriteLine("Terros generated : " + TerrosSequence(5));

существующие ответы направляют вас в правильном направлении, но окончательного ответа нет. Я думал, что подведение итогов и добавление деталей поможет вам и будущим посетителям.

Название задачи

Первоначальное название этого вопроса было "конъюнктура Терроса". Во-первых, это гипотеза , во-вторых, модификация исходной последовательности Коллатца, которую вы использовали, происходит от Riho Terras* (не Terros!), которые доказали Теорема террас говорят это почти для всех t₀ означает, что ∃n ∈ ℕ: t . Вы можете прочитать больше об этом на MathWorld и вопрос chux по математике.ГП.

* в поисках того, кого упоминал Р. Террас в MathWorld, я нашел не только запись на Geni.com , но также вероятный автор этой записи, его племянница Астрид террас, и генеалогия ее семьи. Только для действительно любопытных. ☺

В формула

Вы неправильно поняли формулу в своем вопросе. Как показывает таблица последовательностей для различных t₀, вы должны тестировать на четность из t₋₁ вместо n.

Формула взята из MathWorld.

Также неверен заголовок второго столбца таблицы, он должен читать t₀, t₁, t₂, ..., поскольку t₀ тоже указан.

Вы повторяете ошибку с тестированием n вместо t₋₁ в вашем коде тоже. Если выходные данные вашей программы точно определены (например, при проверке автоматическим судьей), подумайте еще раз, следует ли выводить t₀ или нет.

Целочисленная и плавающая арифметика

При выполнении операции с двумя целыми числами получается целое число. Если задействован поплавок, то результатом будет поплавок. В обеих ветвях вашего условия вы вычисляете выражение такой формы:

1 / 2 * …

1 и 2-целые числа, поэтому деление-это целочисленное деление. Целочисленное деление всегда округляется вниз, поэтому выражение фактически

0 * …

Которая (почти*) всегда равна нулю. Тайна раскрыта. Но как это исправить?

Вместо того, чтобы умножать на одну половину, вы можете разделить на две. В четной ветви деление на 2 не дает остатка. В нечетной ветви t - ₁ нечетно, поэтому 3 · t₋₁ тоже нечетно. Нечетное плюс 1-четное, поэтому деление на два всегда дает остаток, равный нулю в обеих ветвях. Целое число деления достаточно, результат точен.

Кроме того, вы можете использовать деление с плавающей точкой, просто замените 1 на 1.0. Но это, вероятно, не даст правильных результатов. Видите ли, все члены последовательности являются целыми числами, и вы получаете результаты с плавающей точкой! Итак, округление с Math.Round() и приведение к целому числу? Нет... если сможешь, всегда уклоняйся с помощью поплавков. Я думаю, что для них существует очень мало вариантов использования, большинство из которых связано с графикой или численными алгоритмами. В большинстве случаев вы этого не делаете. нужны они, и они просто вводятошибки округления .

* ноль раз все, что может произвести NaN тоже, но давайте проигнорируем возможность того, что "все, что угодно" будет из специальных значений с плавающей точкой. Я просто педантичен.

Рекурсивное решение

Помимо проблем, упомянутых выше, весь ваш рекурсивный подход несовершенен. Очевидно, вы намеревались Terras(n) быть t. Это не так уж и плохо. Но потом вы забыли, что вы поставляете t₀ и ищите n , а не наоборот.

Чтобы исправить свой подход, вам нужно будет установить "глобальную" переменную int t0, которая будет установлена в given t₀ и возвращена из Terras(0). Тогда Terras(n) действительно вернет t. Но вы все равно не будете знать значение n, когда последовательность остановится. Вы могли только повторять для большего и большего n , разрушая временную сложность.

Подождите. Как насчет кэширования результатов промежуточных Terras() звонит в ArrayList<int> t? t[i] будет содержать результат для Terras(i) или ноль, если он не инициализирован. В верхней части Terras() вы бы добавили if (n < t.Count() && t[n] != 0) return t[n]; для немедленного возврата значения, если оно кэшировано и не повторяет вычисление. В противном случае вычисление действительно выполняется и непосредственно перед возвращением результат кэшируется:

if (n < t.Count()) {
    t[n] = return_value;
} else {
    for (int i = t.Count(); i < n; i++) {
        t.Add(0);
    }
    t.Add(return_value);
}

Все еще недостаточно хорошо. Временная сложность сохраняется, но наличие ArrayList увеличивает пространственную сложность. Попробуйте проследить (желательно вручную, карандашом и бумагой) вычисление для t0 = 3; t.Add(t0);. Вы не зная заранее конечного n , вы должны идти от 1 до тех пор, пока Terras(n) не вернет 1.

Заметили что-нибудь? Во-первых, каждый раз, когда вы увеличиваете n и делаете новый вызов Terras(), вы добавляете вычисленное значение в конце кэша (t). Во-вторых, вы всегда смотрите только на один пункт назад. Вы вычисляете всю последовательность снизу вверх, и вам не нужен этот большой глупый ArrayList , но всегда только его последний пункт!

Итерационное решение

Ладно, забудем об этом. сложное рекурсивное решение, пытающееся следовать определению сверху вниз и перейти к подходу снизу вверх, который возник из постепенного улучшения исходного решения. Рекурсия больше не нужна, она просто загромождает все дело и замедляет его.

Конец последовательности все еще находится путем инкрементирования n и вычисления t, останавливаясь, когда t = 1. Переменная t хранит t, t_previous хранит предыдущий t (Теперь t - ₁ ). То отдых должен быть очевиден.

public static void Terras(int t) {
    Console.Write("Terras generated:");
    Console.Write(" " + t);
    while (t > 1) {
        int t_previous = t;
        if (t_previous % 2 == 0) {
            t = t_previous / 2;
        } else {
            t = (3 * t_previous + 1) / 2;
        }
        Console.Write(", " + t);
    }
    Console.WriteLine("");
}

имена переменных взяты из ответа чукса, просто для сравнения.

Это можно считать примитивным примеромметода динамического программирования . Эволюция этого решения является общей для всего класса таких проблем. Медленная рекурсия, кэширование результатов вызовов, динамический подход "снизу-вверх". Когда вы будете более опытны в динамическом программировании, вы начнете видеть его непосредственно даже в более сложных ситуациях. проблемы, даже не думая о рекурсии.