Где я могу найти эффективность O (n) некоторых методов Numpy?

Я делаю школьный проект, и они спросили об эффективности некоторых методов Numpy, и я не могу их найти. Кто-нибудь может сказать мне, где я могу их найти?

Примеры методов, таких как:

numpy.linspace(x,y,z) numpy.meshgrid(x,y) numpy.zeroes(x,y)

1 2
numpy performance processing-efficiency

1 ответ:

Вы можете просто измерить время выполнения для различных размеров задачи, чтобы получить оценку сложности времени,

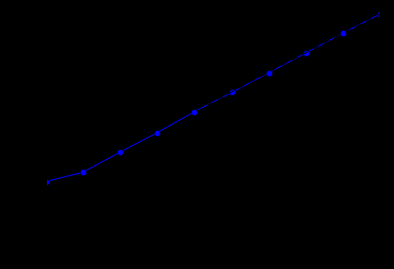
Например, ниже приведен код для измерения временной сложности для numpy.meshgrid(x,y), который может быть использован и для других функций numpy, 

In [1]: import numpy as np
   ...: from time import time
   ...: import matplotlib.pyplot as plt
   ...: from scipy.optimize import curve_fit
   ...: %matplotlib inline
   ...: 
   ...: def complexity_model(x, n, A, C):
   ...:     return A*x**n + C
   ...: 
   ...: problem_size = np.logspace(2, 4, 10)
   ...: 
   ...: res = []
   ...: for N in problem_size:
   ...:     x = np.linspace(0, 1, N)
   ...:     y = x.copy()
   ...:     
   ...:     t0 = time()
   ...:     np.meshgrid(x,y)
   ...:     dt = time() - t0
   ...:     res.append(dt)
   ...: 
   ...: nn = np.logspace(np.log10(problem_size.min()), np.log10(problem_size.max()), 100)  
   ...: 
   ...: time_to_solution = np.asarray(res)
   ...: fig, ax = plt.subplots(1,1)
   ...: ax.loglog(problem_size, time_to_solution, 'o-b')
   ...: 
   ...: mask = problem_size > 100 # ignore initial points
   ...: 
   ...: popt, _ = curve_fit(complexity_model, problem_size[mask],
   ...:                               time_to_solution[mask],
   ...:                               p0=(1.0, 1.0,  0.0) )
   ...: print(popt)
   ...: ax.loglog(nn, complexity_model(nn, *popt), '--k')
   ...: 
   ...: 
   ...: ax.set_xlabel('Problem size: N')
   ...: ax.set_ylabel('Time to solution 
  [  1.94816942e+00   1.40955397e-08  -7.33862899e-04]

, что дает следующую кривую,

Введите описание изображения здесь

Для достаточно большого массива размеры, numpy.meshgrid(x,y) имеет, таким образом, временную сложность O(n**α), с α = 1.95 ≈ 2.

3