Функция в R для группировки линейных объектов в диаграмме рассеяния
У меня есть карта рассеяния, которую я создал с помощью ggplot.
Данные здесь:
Retirees<- data.frame(No_Races = c(11L, 11L, 21L, 12L, 15L, 10L, 23L, 13L, 19L, 11L, 22L, 14L,
17L, 33L, 12L, 45L, 15L, 55L, 22L, 41L, 19L, 16L, 13L, 26L, 23L,
10L, 20L, 44L, 17L, 14L, 21L, 28L, 18L, 11L, 22L, 37L, 26L, 30L,
15L, 23L, 31L, 47L, 12L, 20L, 16L, 36L, 37L, 29L, 21L, 17L, 68L,
56L, 13L, 22L, 27L, 18L, 23L, 14L, 28L, 19L, 24L, 10L, 15L, 20L,
35L, 25L, 36L, 31L, 26L, 21L, 37L, 16L, 32L, 27L, 11L, 22L, 33L,
28L, 17L, 40L, 23L, 35L, 53L, 65L, 12L, 18L, 30L, 66L, 24L, 36L,
48L, 49L, 25L, 63L, 19L, 38L, 32L, 45L, 13L, 26L, 78L, 39L, 52L,
46L, 33L, 20L, 60L, 27L, 34L, 41L, 69L, 14L, 21L, 42L, 28L, 35L,
57L, 50L, 36L, 29L, 22L, 81L, 37L, 15L, 38L, 23L, 46L, 31L, 48L,
16L, 24L, 32L, 57L, 49L, 41L, 33L, 25L, 42L, 17L, 34L, 26L, 35L,
18L, 27L, 54L, 45L, 37L, 28L, 47L, 19L, 57L, 29L, 39L, 10L, 20L,
30L, 40L, 41L, 31L, 21L, 42L, 32L, 54L, 11L, 22L, 33L, 44L, 66L,
67L, 45L, 34L, 23L, 69L, 46L, 35L, 47L, 59L, 71L, 36L, 12L, 24L,
60L, 61L, 37L, 25L, 38L, 51L, 64L, 13L, 39L, 26L, 53L, 80L, 67L,
27L, 68L, 55L, 14L, 42L, 28L, 43L, 58L, 29L, 44L, 74L, 15L, 45L,
30L, 46L, 31L, 47L, 79L, 16L, 32L, 48L, 49L, 33L, 50L, 17L, 34L,
52L, 35L, 53L, 18L, 72L, 36L, 54L, 37L, 56L, 19L, 38L, 39L, 20L,
40L, 61L, 41L, 83L, 21L, 42L, 43L, 65L, 87L, 22L, 45L, 23L, 46L,
93L, 47L, 71L, 24L, 72L, 49L, 25L, 100L, 51L, 26L, 52L, 27L,
54L, 28L, 85L, 57L, 29L, 59L, 30L, 31L, 32L, 96L, 65L, 33L, 67L,
34L, 35L, 36L, 37L, 74L, 38L, 77L, 39L, 40L, 41L, 42L, 43L, 44L,
45L, 46L, 47L, 48L, 49L, 50L, 51L, 52L, 53L, 54L, 55L, 56L, 59L,
60L, 61L, 62L, 64L, 65L, 68L, 69L, 71L, 73L, 77L, 82L, 83L, 92L,
98L),
Perc_Retired = c(54.5454545454545, 45.4545454545455, 42.8571428571429, 41.6666666666667,
40, 40, 39.1304347826087, 38.4615384615385, 36.8421052631579,
36.3636363636364, 36.3636363636364, 35.7142857142857, 35.2941176470588,
33.3333333333333, 33.3333333333333, 33.3333333333333, 33.3333333333333,
32.7272727272727, 31.8181818181818, 31.7073170731707, 31.5789473684211,
31.25, 30.7692307692308, 30.7692307692308, 30.4347826086957,
30, 30, 29.5454545454545, 29.4117647058824, 28.5714285714286,
28.5714285714286, 28.5714285714286, 27.7777777777778, 27.2727272727273,
27.2727272727273, 27.027027027027, 26.9230769230769, 26.6666666666667,
26.6666666666667, 26.0869565217391, 25.8064516129032, 25.531914893617,
25, 25, 25, 25, 24.3243243243243, 24.1379310344828, 23.8095238095238,
23.5294117647059, 23.5294117647059, 23.2142857142857, 23.0769230769231,
22.7272727272727, 22.2222222222222, 22.2222222222222, 21.7391304347826,
21.4285714285714, 21.4285714285714, 21.0526315789474, 20.8333333333333,
20, 20, 20, 20, 20, 19.4444444444444, 19.3548387096774, 19.2307692307692,
19.047619047619, 18.9189189189189, 18.75, 18.75, 18.5185185185185,
18.1818181818182, 18.1818181818182, 18.1818181818182, 17.8571428571429,
17.6470588235294, 17.5, 17.3913043478261, 17.1428571428571, 16.9811320754717,
16.9230769230769, 16.6666666666667, 16.6666666666667, 16.6666666666667,
16.6666666666667, 16.6666666666667, 16.6666666666667, 16.6666666666667,
16.3265306122449, 16, 15.8730158730159, 15.7894736842105, 15.7894736842105,
15.625, 15.5555555555556, 15.3846153846154, 15.3846153846154,
15.3846153846154, 15.3846153846154, 15.3846153846154, 15.2173913043478,
15.1515151515152, 15, 15, 14.8148148148148, 14.7058823529412,
14.6341463414634, 14.4927536231884, 14.2857142857143, 14.2857142857143,
14.2857142857143, 14.2857142857143, 14.2857142857143, 14.0350877192982,
14, 13.8888888888889, 13.7931034482759, 13.6363636363636, 13.5802469135802,
13.5135135135135, 13.3333333333333, 13.1578947368421, 13.0434782608696,
13.0434782608696, 12.9032258064516, 12.5, 12.5, 12.5, 12.5, 12.280701754386,
12.2448979591837, 12.1951219512195, 12.1212121212121, 12, 11.9047619047619,
11.7647058823529, 11.7647058823529, 11.5384615384615, 11.4285714285714,
11.1111111111111, 11.1111111111111, 11.1111111111111, 11.1111111111111,
10.8108108108108, 10.7142857142857, 10.6382978723404, 10.5263157894737,
10.5263157894737, 10.3448275862069, 10.2564102564103, 10, 10,
10, 10, 9.75609756097561, 9.67741935483871, 9.52380952380952,
9.52380952380952, 9.375, 9.25925925925926, 9.09090909090909,
9.09090909090909, 9.09090909090909, 9.09090909090909, 9.09090909090909,
8.95522388059701, 8.88888888888889, 8.82352941176471, 8.69565217391304,
8.69565217391304, 8.69565217391304, 8.57142857142857, 8.51063829787234,
8.47457627118644, 8.45070422535211, 8.33333333333333, 8.33333333333333,
8.33333333333333, 8.33333333333333, 8.19672131147541, 8.10810810810811,
8, 7.89473684210526, 7.84313725490196, 7.8125, 7.69230769230769,
7.69230769230769, 7.69230769230769, 7.54716981132075, 7.5, 7.46268656716418,
7.40740740740741, 7.35294117647059, 7.27272727272727, 7.14285714285714,
7.14285714285714, 7.14285714285714, 6.97674418604651, 6.89655172413793,
6.89655172413793, 6.81818181818182, 6.75675675675676, 6.66666666666667,
6.66666666666667, 6.66666666666667, 6.52173913043478, 6.45161290322581,
6.38297872340426, 6.32911392405063, 6.25, 6.25, 6.25, 6.12244897959184,
6.06060606060606, 6, 5.88235294117647, 5.88235294117647, 5.76923076923077,
5.71428571428571, 5.66037735849057, 5.55555555555556, 5.55555555555556,
5.55555555555556, 5.55555555555556, 5.40540540540541, 5.35714285714286,
5.26315789473684, 5.26315789473684, 5.12820512820513, 5, 5, 4.91803278688525,
4.8780487804878, 4.81927710843374, 4.76190476190476, 4.76190476190476,
4.65116279069767, 4.61538461538461, 4.59770114942529, 4.54545454545455,
4.44444444444444, 4.34782608695652, 4.34782608695652, 4.3010752688172,
4.25531914893617, 4.22535211267606, 4.16666666666667, 4.16666666666667,
4.08163265306122, 4, 4, 3.92156862745098, 3.84615384615385, 3.84615384615385,
3.7037037037037, 3.7037037037037, 3.57142857142857, 3.52941176470588,
3.50877192982456, 3.44827586206897, 3.38983050847458, 3.33333333333333,
3.2258064516129, 3.125, 3.125, 3.07692307692308, 3.03030303030303,
2.98507462686567, 2.94117647058824, 2.85714285714286, 2.77777777777778,
2.7027027027027, 2.7027027027027, 2.63157894736842, 2.5974025974026,
2.56410256410256, 2.5, 2.4390243902439, 2.38095238095238, 2.32558139534884,
2.27272727272727, 2.22222222222222, 2.17391304347826, 2.12765957446809,
2.08333333333333, 2.04081632653061, 2, 1.96078431372549, 1.92307692307692,
1.88679245283019, 1.85185185185185, 1.81818181818182, 1.78571428571429,
1.69491525423729, 1.66666666666667, 1.63934426229508, 1.61290322580645,
1.5625, 1.53846153846154, 1.47058823529412, 1.44927536231884,
1.40845070422535, 1.36986301369863, 1.2987012987013, 1.21951219512195,
1.20481927710843, 1.08695652173913, 1.02040816326531))
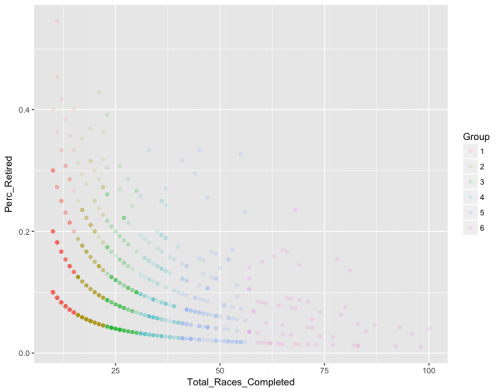
Данные выглядят следующим образом при построении графика
ggplot(Retirees,aes(x=No_Races,y=Perc_Retired)) +
geom_point()
Здесь явно линейные группы - есть ли какие-либо функции в R, которые позволят мне сгруппировать каждую точку в одну из линейных групп.
Я пробовал кластеризацию k-means, но неудивительно, что они не следуют линейным группам:
3 ответа:
Прежде чем я перейду к ответу, я придумал - предупреждение : Убедитесь, что ваши данные не имеют этой формы из-за некоторой дискретизации, лежащей в основе процесса генерации данных, или из-за наличия дискретных значений, которые затем преобразуются в проценты.
Тем не менее, даже если это артефакт, я все равно думаю, что это интересный вопрос. В итоге я создал гибридную линейную регрессию / k-means, которая, как мне кажется, довольно хорошо решает вашу проблему. Я не уверен, что это так. изобретать велосипед или нет, и я уверен, что есть улучшения, которые можно сделать, но я думаю, что это должно работать для вас.Первое замечание (мой выбор дизайна): поскольку вы уже были готовы попробовать k-значит, я придерживаюсь этого типа подхода. По существу, недостатком этого является то, что вам нужно будет выбрать $K$ (количество кластеров). Я бы рекомендовал попробовать несколько значений и посмотреть, какое из них дает вам желаемые результаты.
Второе примечание (местное Оптима и оптимизация) : созданный мною код использует тип "генетического алгоритма" (по крайней мере, я думаю, что это правильное название для него), чтобы преодолеть local-optima. По существу, он выполняет оптимизацию
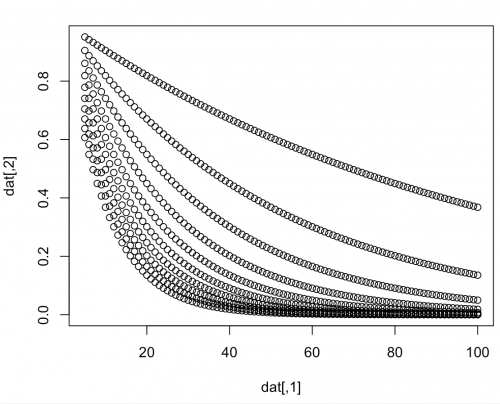
n.unitиз случайных начальных точек одновременно, на каждой итерации он берет худшую оптимизацию и заменяет ее лучшей. По сути, это сокращает время, потраченное впустую на работу с дерьмовыми решениями, застрявшими в локальных оптимумах. Также я использую случайную выборку членства в группе для дальнейшей помощи перебирайтесь через местную Оптиму. Я нахожу, что он работал довольно хорошо на моих смоделированных данных и был довольно быстрым.Во - первых, я смоделировал данные, которые немного похожи на ваши.
library(tidyverse) lambda <- seq(0.01, .1, by=0.01) x <- 5:100 pars <- expand.grid("lambda" = lambda, "x" = x) dat <- cbind(pars$x, exp(-pars$lambda*pars$x)) plot(dat)Второй вход-преобразование данных
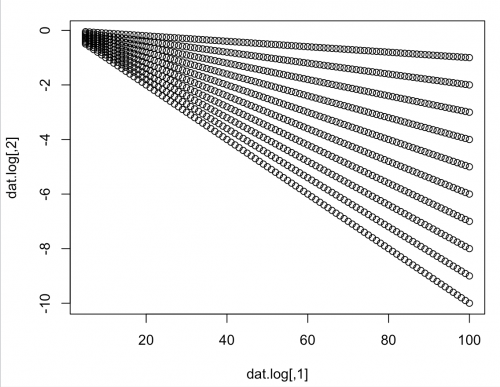
Я бы сначала предложил вам лог-преобразовать ваши значения для
Perc_Retired. Это, вероятно, заставит их выглядеть гораздо более линейными.dat.log <- cbind(dat[,1], log(dat[,2])) plot(dat.log)Третье-собственно "линейная регрессия-к-означает-вещь", которую я приготовил вверх
# Create Design Matrix and Response X <- cbind(1, dat.log[,1]) # Design matrix, add intercept Y <- dat.log[,2] # Responses K <- 10 # Number of Clusters n.unit <- 10 # Number of parallel optimizations to run n <- nrow(X) # Number of observations # Function to convert vector/matrix to probabilities (e.g., normalize to 1) miniclo <- function (c){ if (is.vector(c)) c <- matrix(c, nrow = 1) (c/rowSums(c)) } # Random Initialize the group assignments. gs <- as.list(1:n.unit) %>% map(~sample(1:K, size = nrow(dat.log), replace = TRUE)) n.iter <- 100 # Number of iterations to run the optimization for for (i in 1:n.iter) { # Start out by fitting linear regressons to each group fits <- gs %>% map(~split(1:n, .x)) %>% at_depth(2, ~lm.fit(X[.x,], Y[.x])) # Fit models # Calculate the squared residuals of each data-point to each # groups fitted linear model. Note I also add a small value (0.0001) # to avoid zero values that can show up later when converting to probabilities # and inverting. sq.resids <- fits %>% at_depth(2, "coefficients") %>% # Extract Coefficients at_depth(2, ~((Y-X%*%.x)^2)+0.0001) %>% # Predict and Compute Squared Residuals map(bind_cols) # Store which "unit" which of the n.unit optimiztions did the # best and which did the worst best.worst <- sq.resids %>% map(sum) %>% unlist() best.worst <- c(which.min(best.worst), which.max(best.worst)) # Compute new group assignements, notice I convert the relative # squared residual of each model into a probability and then use the # inverse of this probability as the probability that a data-point # belongs to that group new.gs <- sq.resids %>% map(miniclo) %>% # Add small value to fix zeros map(~.x^(-1)) %>% map(miniclo) %>% map(~apply(.x, 1, function(x) sample(1:K, 1, replace = TRUE, prob = x))) # Add sampling to get over some minima # Replace the worst unit with the best new.gs[[best.worst[2]]] <- new.gs[[best.worst[1]]] # Update the cluster assignemnts for each unit gs <- new.gs } # Now investigate results of best unit and plot pal <- rainbow(10) best.g <- new.gs[[best.worst[1]]] # Function to enable easier plotting of the results. plot_groupings <- function(d, g, col=rainbow(length(unique(g)))){ K <- length(unique(g)) plot(d) for (i in 1:K){ d.local <- d[g == i,] d.local <- d.local[order(d.local[,1]), ] lines(d.local, col = col[i], lwd=2) } }Первый график на логарифмически преобразованном масштабе, на который мы помещаем модель
plot_groupings(dat.log, best.g)Теперь постройте график в исходном масштабе данных
Как вы можете видеть, модель работает довольно хорошо. Небольшое количество очков не классифицируется (это может улучшиться, если вы увеличите либоplot_groupings(dat, best.g)n.unit, либоn.iter, я ставлю), но в целом я вполне доволен результатами.Потенциальные обобщения или Альтернативы
Обратите внимание, что этот подход, использующий квадратные невязки в качестве средства кластеризации k-средних, является довольно общим и будет работать для других моделей (не только линейных моделей). Мне было бы интересно узнать, было ли это сделано раньше (я был бы шокирован, если бы я действительно изобрел что-то новое здесь).Я не слишком много искал в интернете, чтобы найти это. Вы также, вероятно, можете найти что-то хорошее, поискав "функциональную кластеризацию данных" или что-то в этом роде.
В любом случае, надеюсь, это поможет.Обновление: применяется к предоставленным вами данным
Я применил свою модель к данным, которые вы предоставили, с той лишь разницей, что я также преобразовал переменную No_Races (а не только переменную Perc_Retired) для линеаризации данных.
Я думаю, что результаты намного лучше, чем dbscan.
Слишком долго для комментария, поэтому я публикую его в качестве ответа.
У меня сложилось впечатление, что для такого рода задач,
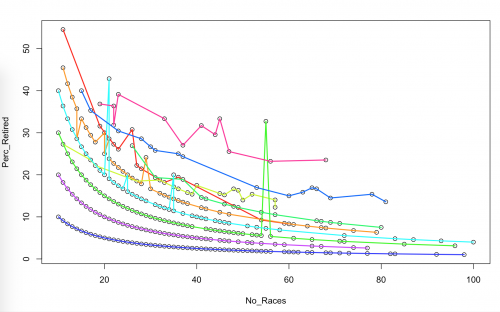
dbscanработает хорошо. Смотрите, например, здесь для хорошей визуализации различных алгоритмов кластеризации и их производительности. DBSCAN реализован в R в одноименном пакете. Смотритездесь для виньетки. Излишне говорить, что вам нужно настроить некоторые параметры, но после примерно минуты возни, я произвел следующее:Это явно не идеально, но эй, я потратил на это около минуты. Я уверен, что вы можете улучшить это с соответствующей настройкой параметров.library(dbscan) db <- dbscan(Retirees, eps = 2, minPts = 3) plot(Retirees, col = db$cluster + 1L, pch = db$cluster + 1L)
Причина, по которой это не сработало, заключается в том, что вы забыли масштабировать Данные соответствующим образом.
Однако у меня для вас плохие новости:
Это не кластеры, а артефакты. Очевидно, что некоторые данные были дискретизированы в какой-то момент до преобразования, поэтому вы получаете эти уродливые артефакты. Они не реальны.Обратите внимание, что линии следуют за 1/x, 2/x и т. д.
Точно, отмените проценты . Тогда вы увидите, что у вас есть "кластеры", где 1, 2, 3, имеют в отставке. Бесполезные "кластеры", когда речь заходит о поиске чего-то нового.