DFA к математической нотации

Предположим, у меня есть DFA с алфавитом {0,1}, который в основном принимает любые строки, пока нет последовательных 0 (не более одного 0 за раз). Как мне выразить это в математической нотации?

Я имел в виду любое число 1, за которым следует либо один, либо ни одного 0, а затем любое число 1..... но никак не мог придумать для него подходящую математическую нотацию.

Моя попытка, но явно неверная, так как 1010 должен быть принят, но обозначение не указывает так: этот

1 2
computer-science finite-automata

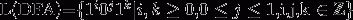
1 ответ:

В качестве регулярного выражения вы можете записать это как 1*(01+)*0?. Произвольное множество единиц, затем произвольное множество групп ровно из одного нуля, за которыми следует по крайней мере один ноль, и в конце концов, возможно, один ноль. Нико уже написал об этом в комментарии. Лично я считаю такое регулярное выражение достаточно формальным, чтобы назвать его математическим.

Теперь, если вы хотите написать это, используя экспоненты, вы можете сделать что-то вроде

L = {1а (0 11+bя ... ) с 0d mod 2 | a, b i , c, d ∈ ℕ для 1 ≤ i≤c }

Написание немного формулы в экспонентах имеет большое преимущество, что вам не нужно разделять место, где вы используете экспоненту и место, где вы определяете диапазон. Здесь все мои числа являются натуральными числами (включая ноль). Добавление одного означает, по крайней мере, одно повторение. А по модулю 2 получается показатель степени 0 или 1 для выражения ? в регулярном выражении.

Конечно, здесь есть подразумеваемое предположение, а именно, что c служит своего рода циклом, но он не повторяет одно и то же выражение каждый раз, а bя ... изменения для каждой итерации. Диапазон i подразумевает эту интерпретацию, но тем не менее ее можно считать запутанной или даже неправильной.

Правильным решением здесь было бы использование некоторого формального обозначение продукта с использованием большого ∏ с подстрочным индексом i = 1 и надстрочным индексом c. Это означало бы, что для каждого i от 1 до c требуется вычислить данное выражение (т. е. 011+bя ... ) и объедините все полученные слова.

Можно также дать рекурсивное определение: минимальная точка фиксации следующего определения

L' = {1, 10} ∪ {1а 0 b | a ∈ ℕ, a > 0, b ∈ L'}

- это язык всех слов, которые начинаются с 1 и удовлетворяют вашим условиям. Из этого можно построить

L = {ε, 0} ∪ L' ∪ {0 а | а ∈ L'}

Таким образом, вы добавляете пустое слово и одинокий ноль, а затем берете все слова из L' в их неизмененной форме и в форме с нулем, добавленным спереди.
1