Что быстрее: вставка в приоритетную очередь или ретроспективная сортировка?

Это, вероятно, приходит к вам немного поздно в игре, Что касается вашего вопроса, но давайте будем полными.

Тестирование-лучший способ ответить на этот вопрос для конкретной архитектуры компьютера, компилятора и реализации. Кроме того, существуют обобщения.

Во-первых, очереди приоритетов не обязательно O(N log n).

Если у вас есть целочисленные данные, существуют очереди приоритетов, которые работают за O (1) Время. Публикации Beucher и Мейера 1992 года " морфологический подход к сегментации: преобразование водораздела " описывает иерархические очереди,которые довольно быстро работают для целых значений с ограниченным диапазоном. Публикация Брауна 1988 года "очереди календаря: быстрая реализация очереди приоритетов 0 (1) для задачи набора событий моделирования" предлагает другое решение, которое хорошо справляется с большими диапазонами целых чисел - два десятилетия работы после публикации Брауна дали некоторые хорошие результаты для выполнения очередей приоритетов целых чисел быстро. Но механизм этих очередей может усложниться: сортировка по ковшам и сортировка по радиусам все еще могут обеспечивать работу O(1). В некоторых случаях вы даже можете квантовать данные с плавающей запятой, чтобы воспользоваться преимуществами очереди приоритетов O (1).

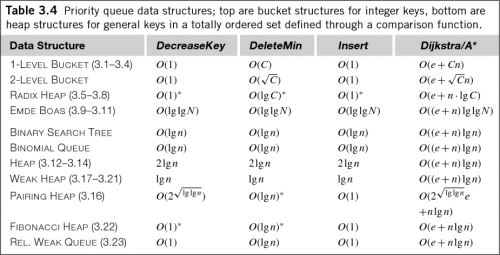
Даже в общем случае данных с плавающей запятой, что O (N log n) немного вводит в заблуждение. В книге эделькампа "эвристический Поиск: теория и приложения" есть следующая удобная таблица, показывающая временную сложность для различных алгоритмов очереди приоритетов (помните, приоритетные очереди эквивалентны сортировке и управлению кучей):

Как вы можете видеть, многие приоритетные очереди имеют O (log n) затраты не только на вставку, но и на извлечение, и даже на управление очередями! Хотя коэффициент обычно снижается для измерения временной сложности алгоритма, эти затраты все же стоит знать.

Но все эти очереди все еще имеют временные сложности, которые сопоставимы. Что лучше всего? Статья Криса л. Луэнго Хендрикса за 2010 год этот вопрос рассматривается в разделе "пересмотр очередей приоритетов для анализа изображений".

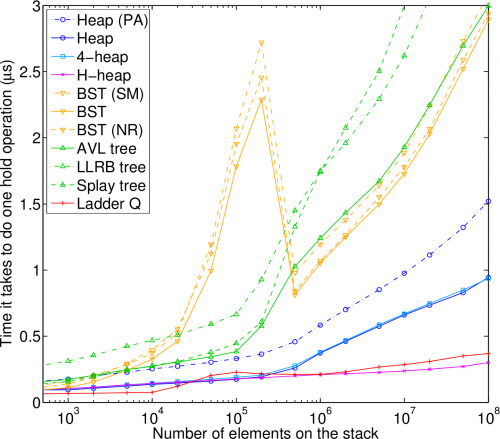
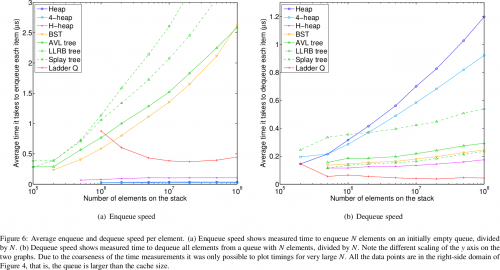
В тесте удержания Хендрикса приоритетная очередь была заполненаN случайными числами в диапазоне [0,50]. Затем самый верхний элемент очереди был удален из очереди, увеличенный случайным значением в диапазоне [0,2], а потом встали в очередь. Эта операция была повторена.10^7 времена. Накладные расходы на генерацию случайных чисел вычитались из измеренного времени. Лестница очереди и иерархические нагромождения довольно хорошо справились с этим тестом.

Было также измерено время на элемент для инициализации и опустошения очередей-эти тесты очень важны для вашего вопроса.

Как вы можете видеть, различные очереди часто имели очень разные ответы на запросы и удаления из очереди. Эти цифры подразумевают, что, хотя могут существовать алгоритмы приоритетной очереди, которые превосходят непрерывную работу, нет лучшего выбора алгоритма для простого заполнение и последующее опустошение приоритетной очереди (операция, которую вы выполняете).

Давайте вернемся к вашим вопросам:

что быстрее: вставка в приоритетную очередь или ретроспективная сортировка?

Как показано выше, приоритетные очереди можно сделать эффективными, но все еще существуют затраты на вставку, удаление и управление. Вставка в вектор происходит быстро. Это O(1) в амортизированном времени, и нет никаких затрат на управление, плюс вектор O (n) должен быть читать.

Сортировка вектора будет стоить вам O (n log n) при условии, что у вас есть данные с плавающей запятой, но на этот раз сложность не скрывает такие вещи, как очереди приоритетов. (Впрочем, надо быть немного осторожнее. Quicksort работает очень хорошо на некоторых данных, но он имеет наихудшую временную сложность O(n^2). Для некоторых реализаций это серьезная угроза безопасности.)

Боюсь, что у меня нет данных о затратах на сортировку, но я бы сказал, что ретроактивная сортировка отражает суть из того, что вы пытаетесь сделать лучше и, следовательно, лучший выбор. Исходя из относительной сложности управления очередью приоритетов по сравнению с последующей сортировкой, я бы сказал, что последующая сортировка должна быть быстрее. Но опять же, вы должны проверить это.

я генерирую некоторые элементы, которые мне нужно отсортировать в конце. Мне было интересно, что быстрее с точки зрения сложности: вставка их непосредственно в приоритетную очередь или аналогичную структуру данных, или использование алгоритма сортировки в конце?

Мы вероятно, об этом говорилось выше.

Но есть еще один вопрос, который ты не задал. И, возможно, вы уже знаете ответ. Это вопрос стабильности. В C++ STL говорится, что приоритетная очередь должна поддерживать "строгий слабый" порядок. Это означает, что элементы с равным приоритетом несравнимы и могут быть размещены в любом порядке, в отличие от "общего порядка", где каждый элемент сопоставим. (Здесь есть хорошее описание порядка .) В сортировке "строгий слабый" аналогичен неустойчивая сортировка и" полный порядок " аналогичны стабильной сортировке.

В результате получается, что если элементы с одинаковым приоритетом должны оставаться в том же порядке, в котором вы их поместили в структуру данных, то вам нужна стабильная сортировка или полный порядок. Если вы планируете использовать C++ STL, то у вас есть только один вариант. Приоритетные очереди используют строгий слабый порядок, поэтому они здесь бесполезны, но алгоритм" stable_sort " в библиотеке алгоритмов STL выполнит эту работу.

Надеюсь, это поможет. Позвольте мне знайте, если вы хотите получить копию любого из упомянутых документов или хотели бы получить разъяснения. :- )

На ваш первый вопрос (который быстрее): это зависит. Просто проверьте это. Предполагая, что вы хотите получить конечный результат в векторе, альтернативы могут выглядеть примерно так:

#include <iostream>
#include <vector>
#include <queue>
#include <cstdlib>
#include <functional>
#include <algorithm>
#include <iterator>

#ifndef NUM
    #define NUM 10
#endif

int main() {
    std::srand(1038749);
    std::vector<int> res;

    #ifdef USE_VECTOR
        for (int i = 0; i < NUM; ++i) {
            res.push_back(std::rand());
        }
        std::sort(res.begin(), res.end(), std::greater<int>());
    #else
        std::priority_queue<int> q;
        for (int i = 0; i < NUM; ++i) {
            q.push(std::rand());
        }
        res.resize(q.size());
        for (int i = 0; i < NUM; ++i) {
            res[i] = q.top();
            q.pop();
        }
    #endif
    #if NUM <= 10
        std::copy(res.begin(), res.end(), std::ostream_iterator<int>(std::cout,"\n"));
    #endif
}

$ g++     sortspeed.cpp   -o sortspeed -DNUM=10000000 && time ./sortspeed

real    0m20.719s
user    0m20.561s
sys     0m0.077s

$ g++     sortspeed.cpp   -o sortspeed -DUSE_VECTOR -DNUM=10000000 && time ./sortspeed

real    0m5.828s
user    0m5.733s
sys     0m0.108s

Итак, std::sort удары std::priority_queue, в данном случае . Но, возможно, у вас есть лучшая или худшая std:sort, и, возможно, у вас есть лучшая или худшая реализация кучи. Или, если не лучше или хуже, просто более или менее подходит для вашего точного использования, которое отличается от моего изобретенного использования: "создайте сортированный вектор, содержащий значение".

Я могу с большой уверенностью сказать, что случайные данные не попадут в худший случай std::sort, поэтому в некотором смысле этот тест может льстить ему. Но для хорошей реализации std::sort, ее худший вариант будет очень трудно построить, и может быть не так уж плохо в любом случае.

Edit: я добавил использование мультинабора, так как некоторые люди предложили дерево:

    #elif defined(USE_SET)
        std::multiset<int,std::greater<int> > s;
        for (int i = 0; i < NUM; ++i) {
            s.insert(std::rand());
        }
        res.resize(s.size());
        int j = 0;
        for (std::multiset<int>::iterator i = s.begin(); i != s.end(); ++i, ++j) {
            res[j] = *i;
        }
    #else

$ g++     sortspeed.cpp   -o sortspeed -DUSE_SET -DNUM=10000000 && time ./sortspeed

real    0m26.656s
user    0m26.530s
sys     0m0.062s

К вашему второму вопросу (сложность): они все O (N log n), игнорируя детали реализации fiddly например, является ли выделение памяти O(1) или нет (vector::push_back и другие формы вставки в конце амортизируются O(1)) и предполагая, что под "сортировкой" вы подразумеваете сортировку сравнения. Другие виды рода могут иметь меньшую сложность.

Зависит от данных, но я обычно нахожу InsertSort более быстрым.

У меня был связанный с этим вопрос, и я обнаружил, что в конце концов узким местом было то, что я делал дефферентную сортировку (только когда мне это было нужно), и на большом количестве элементов у меня обычно был наихудший сценарий для моего QuickSort (уже в порядке), поэтому я использовал вставку сортировки

Сортировка 1000-2000 элементов с большим количеством пропусков кэша

Так что анализируйте свои данные!

Насколько я понимаю, ваша задача не требует приоритетной очереди, так как ваши задачи звучат как "сделайте много вставок, после этого отсортируйте все". Это все равно что стрелять в птиц из лазера, а не из подходящего инструмента. Используйте для этого стандартные методы сортировки.

Вам понадобится приоритетная очередь, если ваша задача-имитировать последовательность операций, где каждая операция может быть либо "добавить элемент в набор", либо "удалить наименьший/наибольший элемент из набора". Это можно использовать в задача нахождения кратчайшего пути на графике, например. Здесь нельзя просто использовать стандартные методы сортировки.

Приоритетная очередь обычно реализуется в виде кучи. Сортировка с помощью кучи в среднем медленнее, чем quicksort, за исключением того, что quicksort имеет худшую производительность в худшем случае. Кроме того, кучи-это относительно тяжелые структуры данных, поэтому накладных расходов больше.

Я бы рекомендовал сортировку в конце.

Почему бы не использовать бинарное дерево поиска? Затем элементы сортируются в любое время, и затраты на вставку равны приоритетной очереди. Читайте о сбалансированных деревьях RedBlack здесь

Я думаю, что вставка более эффективна почти во всех случаях, когда вы генерируете данные (т. е. еще не имеете их в списке).

Приоритетная очередь-это не единственный вариант вставки по ходу работы. Как уже упоминалось в других ответах, бинарное дерево (или связанное с ним RB-дерево) одинаково эффективно.

Я бы также проверил, как реализуется приоритетная очередь - многие уже основаны на b-деревьях, но некоторые реализации не очень хорошо извлекают элементы (они по сути, пройдите всю очередь и найдите наивысший приоритет).

На очереди с максимальным приоритетом вставки выполняются операции O (lg n)