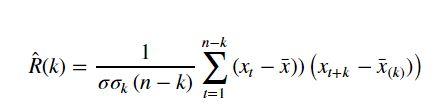Автокорреляция для нестационарных временных рядов

Я реализовал функцию в python для вычисления автокорреляции временного ряда с определенным запаздыванием k. она реализована в предположении, что некоторые временные ряды не могут быть стационарными. Однако я нахожу, что для некоторых из них я получаю значения больше 1, особенно на последних лагах. Так что, наверное, я ошибаюсь в каких-то расчетах.

Я реализую следующее:

Введите описание изображения здесь

Где для терминов в соответствии с запаздывающим рядом я вычисляю среднее и стандартное отклонение от лага k и далее.

Я реализовал следующий код в python, который вычисляет автокорреляцию для конкретного лага k: 

def custom_autocorrelation(x, lag = 12):
    n = len(x)
    std = x.std()
    mu = x.mean() 
    autocov = 0
    mu_lag = x[lag:].mean() 
    std_lag = x[lag:].std() 
    for j in range(n-lag):
        autocov += (x[j] - mu)*(x[j+lag] - mu_lag)
    autocorr = autocov/(std*std_lag*(n-lag))
    return autocorr

В качестве примера я пытаюсь со следующей последовательностью, для k = 12, получить коэффициент 1,03: 

np.array([20623., 11041.,  5686.,  2167.,  2375.,  2057.,  3141.,   504.,
         152.,  6562.,  8199., 15103., 16632.,  7190.,  6987.,  2652.,
        1949.,  2223.,  1703.,  2163.,  1850.,  6932.,  5932., 13124.,
       14846.,  7850.,  4526.,  1277.,  1036.,  1500.,  1648.,  1384.,
        1446.,  3477.,  6818., 12446.,  9734.])

Любая помощь будет очень признательна!

1 2
python time-series

1 ответ:

Я думаю, что вы просто неправильно записали уравнение. Следующие части 

std = x.std()
mu = x.mean()

Не соответствуют оригиналу документа. Похоже, что вам требуется 

std = x[: n - lag].std()
mu = x[: n - lag].mean()

Исправление этого дает 

In [221]: custom_autocorrelation(a, 12)
Out[221]: 0.9569497673729846

Я также взял некоторые идеи из моего предыдущего ответа , чтобы значительно ускорить вычисление 

def modified_acorr(ts, lag):
    """An autocorrelation estimation as per
    http://itfeature.com/time-series-analysis-and-forecasting/autocorrelation-time-series-data

    Args:
        ts (np.ndarray): series
        lag (int): the lag

    Returns:
        float: The autocorrelation
    """
    return (
        (ts[:ts.size - lag] - ts[:ts.size - lag].mean()) *
        (ts[lag:] - ts[lag:].mean())
    ).ravel().mean() / (ts[lag:].std() * ts[:ts.size - lag].std())

Сравнивая регулярную автокорреляционную функцию, мы получаем аналогичные ответы 

In [197]: modified_acorr(a, 12)
Out[197]: 0.9569497673729849

In [218]: acorr(a, a.mean(), 12) / acorr(a, a.mean(), 0)  # normalisation
Out[218]: 0.9201920561073853
1