Antlr4: вычисление математических функций f(x)
В последние дни я работал над своей грамматикой, чтобы иметь возможность вычислять нормальные выражения, такие как: 2+2*5; 2^2 или установить переменные типа y=5+5 и т. д.
Теперь я хочу разобрать функции, такие как f (a, b)=2*a*b; а затем вызвать их позже, как f(5,7); У меня есть некоторые проблемы с этим.
Итак, предположим, что я пытаюсь разобрать объявление функции следующим образом:
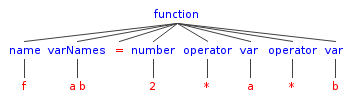
function:name=Var'(' varNames=(MultVar|Var) ')' '=' (Var|Number) (operator=('*'|'/'|'+'|'-') (Var|Number))* SEMI;
Так что это (вроде) работает, но я думаю, что это своего рода "грязно" или что-то еще. Так что я работаю со слушателем, и когда я в "exitFunction" я не знаю, как лучше всего справиться с функцией, поэтому я могу оценить такие вещи, как f(5,7); очень легко.
У меня есть Java-класс под названием " Function.java " с помощью метода "public double eval(double... args)"
Так что прямо сейчас у меня есть строка атрибутов arguments; String expression; String name;, а затем мне нужно провести много времени в слушателе и попытаться найти правильные аргументы и т. д. В строке. Так много подстрок (), и indexOf () и т. д. просто пытаются найти имя, Аргументы и выражение. Затем я сохраняю функцию в хэш-карте.
В моем синтаксическом анализаторе вызов функций выглядит следующим образом:
functioncall: name=Vart '('para=(MultipleNumbers) ')' SEMI;
Кратными числами будут:
MultipleNumber: Number(',' Number)+;
В Лексере. Поэтому я пытаюсь извлечь аргументы из строки и заменить их в функции. Тогда у меня есть нормальное выражение, которое моя программа может решить снова.
Поскольку это кажется мне слишком сложным и почти невозможно получить все правильные "подстроки" и т. д., Я думаю, что должен быть лучший способ реализовать такие вещи. Особенно когда я этого хочу. такие вещи, как: f(a,b)=2*a+b; a=5; f(a,5)
С уважением
Фелрпи
1 ответ:
Один из способов сделать это-разбить ваше конкретное синтаксическое дерево на абстрактное синтаксическое дерево. Затем объект функции сохраняет AST и анализирует его при вызове, что обычно намного проще. Учитывая ваш пример,
f(a, b) = 2 * a * b, это было бы разбито на аналогичное конкретное синтаксическое дерево:Конечно, вы можете это хорошо понять, но это не так просто разобрать! Выражение
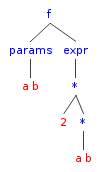
2 * a * bзаписывается в значительной степени как строка, вы не совсем знаете приоритет оператора, глядя у дерева (означает ли2 + a * b2 + (a * b)или(2 + a) * b?) и потребуется некоторое время, чтобы пересечь его в правильном порядке. Однако мы можем разобрать его только один раз, чтобы построить что-то более надежное, более легкое для понимания машины:
О да, теперь это действительно легко разобрать: его вызывают с параметрами
params.length, вы устанавливаете их в хэш-карту или что-то, представляющее вашу область, затем вы вызываете "функцию"*с параметрами2и выражением*(a,b), которое является другая функция, поэтому мы называем ее, передаваяaиbв "функцию"*. Конечно, это легко расширяется для пользовательских функций.Рассматривая функцию
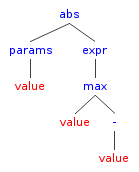
abs (value) = max(value, -value), мы построим АСТ, подобный:
Разбор AST прост, ОК. Но как насчет того, чтобы построить его? Не слишком сложно, если рассматривать все операторы как функции (большинство типа
(num, num) -> num, некоторые (унарные) типа(num) -> num). У нас есть очень стабильное определение для узла в этом дерево:Это может быть чрезмерным упрощением, но это хорошая отправная точка. Как вы заметили, уinterface AstNode { double eval(Scope scope); // you can look at scope as a HashMap<String, double> } class TerminalNode : AstNode { String varName; double constantValue; public TerminalNode(String varName) { this.varName = varName; } public TerminalNode(double constantValue) { this.constantValue = constantValue; this.varName = null; } public double eval(Scope scope) { if (varName == null) return constantValue; return scope.get(varName); } } class CallNode : AstNode { Function target; String[] parameters; AstNode[] children; public CallNode(Function target, String[] parameters, AstNode[] children) { this.target = target; this.parameters = parameters; this.children = children; } public double eval(Scope scope) { double[] subExpressions = new double[children.length]; Scope innerScope = new Scope(scope); // creates a copy for (int i = 0; i < children.length; i++) { // I'm using the copy here because of the edge-case: f(x) = g(x) + x; g(x) = x * 2; // In this case, the x variable is overriden in the innerScope when we resolve g(x) // but we "stored" the previous x value in the "outerScope" so we can add it later subExpressions[i] = children[i].eval(scope); innerScope.set(target.getParamName(i), subExpressions[i]); } // usually, you could do target.getNode().eval(innerScope) // however, this would limit the target function to only be user-defined functions // we leave this way so you can override the Function's eval method to a built-in return target.eval(innerScope); } }CallNodeесть другиеAstNodeпотомки, поэтому это немного бесконечная рекурсия, нарушенная, когда каждый ребенок являетсяTerminalNode(переменная или константа). Как указано в коде, вы можете построить свои операторы как члены классаFunction, либо путем создания экземпляра, либо путем расширения класса. Конечно, это зависит от вашей реализацииFunction. Другой способ-построить другой классAstNode,BuiltinNode(или даже все узлыPlusNode,DivideNode, и т.д.) Для решения вызова с использованием примитивов.
Добавляя это, чтобы ответить на комментарий, "как использовать построенный AST". Предположим, у вас есть объект
Для этого мы используем объектFunctionс именемg, который хранит AST для выраженийf(x, y) = 2 * a * b. Как достичь значенияf(4, 2)?Scope(илиHashMap<String, double>, если это имеет значение). Мы создаем область видимости для функции, где были определены ее параметры, а затем вызываем ее с помощью АСТ, которая будет использовать эту сферу для своих внутренних уровней.Код может выглядеть примерно так:
Scope scope = new Scope(); scope.set("x", 4); scope.set("y", 2); // remember I stored the function f on the object g, just to make a distinction // also, note this is equivalent to g.getNode().eval(scope), because the function stored in g is not a built-in! System.out.println(g.eval(scope));Чтобы решить этот
evalзапрос, AST заранее будет иметь область{x: 4, y: 2}(мы ее создали) и вызовет функцию*(a, b), сa=2иb=x*y. Для решения первого вызова функции*необходимо решить оба ее аргумента (aиb). Решитьaлегко, потому что это терминальный узел (evalнемедленно вернет терминал). Чтобы решитьb, нам нужно вызовите оценку внутренней функции, генерируя новую область{x: 4, y: 2, a: x, b: y}, гдеaиbявляются аргументами второй функции*. Иa, иbбудут решаться как конечные узлы, тогда второй вызов*может вычислить его значение (с помощью встроенной функции, которая вычисляет4*2=8) и верните его вызывающему объекту, который былbдля первой функции*.Теперь имеет область видимости
{x: 4, y: 2, a: 2, b: 8}, гдеxиy- параметрыfиaиbявляются аргументами функции*. При всех заданных аргументах мы можем вызвать встроенную функцию*, дающую16, которая является результатом функции!изображения, генерируемые http://ironcreek.net/phpsyntaxtree