анимация 3d-графика с некоторыми дополнительными требованиями в mathematica

Я написал в этот пост раньше, но я все еще не мог полностью решить следующую проблему. В качестве примера: 

{pA, pB, pC, pD} = {{0, 0, Sqrt[61/3]}, {Sqrt[7], 4*Sqrt[2/3], 0}, {0, -5*Sqrt[2/3], 0}, {-Sqrt[71], 4*Sqrt[2/3], 0}};
axis={1,0,0};pt={0,1,0};
plotPolygon[{a_, b_, c_}] := {Opacity[.4], Polygon[{a, b, c}]};
graph=Graphics3D[{plotPolygon[{pA, pB, pC}], plotPolygon[{pA, pB, pD}], 
            plotPolygon[{pB, pC, pD}], plotPolygon[{pA, pC, pD}]}, 
            Axes -> True, AxesOrigin->pt];
Animate[graph/.gg : Graphics3D[___] :> Rotate[gg, theta, axis], {theta, 0., 2.*Pi}]

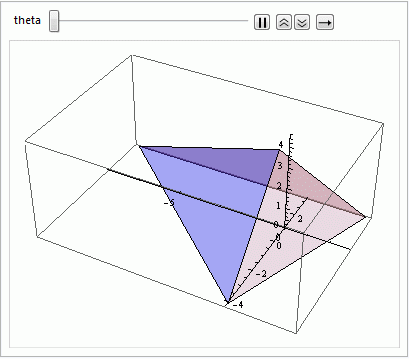
Введите описание изображения здесь

Я хочу вращаться вдоль оси axis={1,0,0}, которая проходит через точку pt={0,1,0}. Но я не знаю, как конкретизировать информацию о точке. Кроме того, анимация вращения кажется очень хаотичной в том смысле, что я ожидал бы, по крайней мере, одну точку (в данном случае, начало координат?) не вращается.

1 3
wolfram-mathematica

1 ответ:

Вам нужно сначала изменить начало координат вершин вашего многоугольника, повернуть и перевести обратно. Вы можете сделать это вручную 

(RotationMatrix[theta,axis].(#-pt) + pt)& /@ {pA, pB, pC, pD}

Или, вы можете объединить преобразования, используя композицию 

Composition[
 AffineTransform[{RotationMatrix[theta,axis],pt}],TranslationTransform[-pt]
] /@ {pA, pB, pC, pD}
Или вы можете взять предыдущую композицию и применить ее непосредственно к вашему объекту Graphics 
GeometricTransformation[ <graphics>, Composition[ ... ]]

Этадокументация дает исчерпывающий список того, что можно сделать.

Edit : вот рабочая анимация сценарий 

Animate[
  graph /. Graphics3D[prims__, opts : OptionsPattern[]] :> 
    Graphics3D[
      GeometricTransformation[prims,
        Composition[
          AffineTransform[{RotationMatrix[theta, axis], pt}],
          TranslationTransform[-pt]
        ]
      ],
      opts
    ], 
  {theta, 0., 2.*Pi}
]

Есть пара вещей, чтобы отметить здесь. Во-первых, GeometricTransformation работает только на самих примитивах, поэтому мне пришлось отделить примитивы от вариантов в Graphics3D с помощью правила Graphics3D[prims__, opts : OptionsPattern[]]. Кроме того, само преобразование должно быть в пределах Animate, чтобы использовать локальную версию theta.

4