алгоритм-как решить арифметическое выражение DAG?

В руководстве по разработке алгоритма есть два связанных акциза.

В принципе, я знаю, как решить первый акциз, но я не знаю, как решить второй , используя решение первого в качестве подсказки.

Акциз арифметического выражения дерево

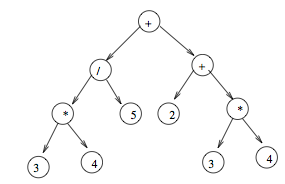
дерево арифметических выражений

Выше приведено дерево арифметических выражений. Предположим, арифметика выражение дано в виде дерева. Каждый лист является целым числом и каждый внутренний узел-это одна из стандартных арифметических операций (+,-,∗,/). Например, выражение 2 + 3 ∗ 4 + (3 ∗ 4)/5 есть представленное деревом на рисунке выше. Дайте алгоритм O(n) для вычисление такого выражения, в котором в дереве имеется n узлов.

Хорошо, это не трудно. Мое решение выглядит так: 

    public float evaluate() {
        return evaluate(root);
    }

    private float evaluate(Node_EX _node) {
        if (_node.left == null || _node.right == null)
            return Float.parseFloat(_node.key);
        String op = _node.key;
        if (op == "+") {
            return evaluate(_node.left) + evaluate(_node.right);
        } else if (op == "-") {
            return evaluate(_node.left) - evaluate(_node.right);
        } else if (op == "*") {
            return evaluate(_node.left) * evaluate(_node.right);
        } else {
            return evaluate(_node.left) / evaluate(_node.right);
        }
    }

Я просто использую рекурсивный способ для решения дерева выражений для результата.

Акциз арифметического выражения Даг

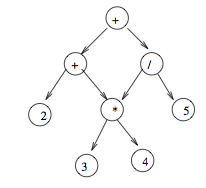
арифметическое выражение dag

Предположим, что арифметическое выражение задано как DAG (направленный ациклический график) с удаленными общими подвыражениями. Каждый лист является целым числом и каждый внутренний узел является одной из стандартных арифметических операций (+,-,∗,/). Например, выражение 2 + 3 ∗ 4 + (3 ∗ 4)/5 есть представлен DAG на рисунке выше. Дайте алгоритм O(n + m) для оценки такой DAG, где в системе имеется n узлов и m ребер ДАГ. подсказка: измените алгоритм для случая дерева для достижения желаемая эффективность.

Хорошо, в описании есть такая подсказка: подсказка: модифицируйте алгоритм для случая дерева, чтобы достичь желаемой эффективности.

На самом деле я совершенно сбит с толку этим намеком. Для типичного дерева, связанного с вещью, мы обычно можем использовать рекурсивное решение. Однако, если это график, мой первый интуитивный подход-использовать BFS или DFS для его решения. Тогда как я могу связать BFS или DFS с деревом, хотя DFS является на самом деле рекурсивный?

2 8
algorithm data-structures directed-acyclic-graphs

2 ответа:

Я полагаю, что для достижения желаемой эффективности задача хочет, чтобы вы избегали переоценки частей дерева, которые вы уже посетили. После того как вы достигли и оценили некоторое поддерево в DAG (каждый узел в дереве представляет поддерево, коренящееся в этом узле), вы можете сохранить полученное значение и связать его с этим поддеревом. Затем, когда вы посетите его снова, вы можете проверить, предварительно ли вы вычислили это значение и просто получить его, а не оценивать его снова.

Есть существует множество различных способов хранения и извлечения этих значений, простой из которых заключается в изменении структуры узла для обеспечения кэшируемого результата.

10

Задача может быть решена с помощью DFS на данном DAG.

  • Мы сохраним повторные вычисления на общих частях аэртметического выражения.

  • Например: при выполнении DFS, когда * будет повторно обнаружен из узла ( / ). Ребро между ( / ) и * является перекрестным ребром, Что означает, что левое и правое поддеревья ( * ) уже вычислены. Таким образом мы воспользуемся этим и сэкономим на пересчете.

  • Однако добиться это нам нужно, чтобы сохранить результаты операции на узлах.

  • Сложность составляет O (n+m), так как это обычный обход DFS с некоторой дополнительной памятью, используемой для хранения промежуточных результатов.

Надеюсь, это поможет.

2